Reference no: EM13818579

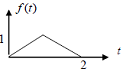
Q.1. Derive the Laplace transform of the sketched f (t) below:

Q.2. Find the inverse Laplace transform of the following functions:

(i) s/L²s² + n²Π^{2 (ii)} 1/(s + √2)(s - √3)

Q. 3. Using Λ[f(t)'] = sF(s) - f(0),

Show that Λ[sin² t] = 2/s(s² +4).

Q.4 Solve the following initial value problem by the Laplace transform:

y'' + 2y' - 3y = 6e^-2t, y(0) = 2, y'(0) = -14 .

Q.5 (a) Iff(t) has the Laplace transform F(s), then show that

Λ{f (t - a) u(t - a)} = e^-asF(s),

where u(t) is a step function.

(b) Find the inverse transform of e^-3s/s³ .

Q6. Using the Laplace transform. solve the following problem.

y'' + 2y' - 3y = 8e^-t + δ(t -1/2 ), y(0) = 3, y'(0)= -5.

Q7. By differentiation, find the inverse Laplace transform of:

s² - Π²/(s² + Π²)²

Q. 8 By differentiation, find the Laplace transform of:

t² cashΠ

Q.9 Using Laplace transforms solve the following integral equation:

y(t) = sin2t + ₀∫¹y(t') sin 2(t -t')dt'

Q. 10: Evaluate the following integral:

_C∫ = 2z³ + z² + 4/z⁴ + 4z² dz,

Where C is the circle |z-2| = 4 clockwise.