Reference no: EM13465

1. We want to find the integral of a function at an arbitrary location x from the origin.  Thus,

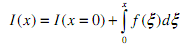
where I(x=0) is the value of the integral for all times less than 0.  (Essentially, I(x=0) is the unknown constant of integration or the initial condition.)  From the class lecture on the trapezoidal rule for numerical integration, it can be seen that this function can be approximated by

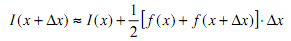
Write a Matlab function to perform numerical integration of a set of evenly spaced data points using the trapezoidal rule.  Your function should accept two vectors as inputs, x and f.  The first vector (x) contains the independent variable data (the points at which the values of the function are known.  The second vector (f) should contain the values of the function at the points provided in the first vector.  Your function should return the integral of f with respect to x, as a function of x.

2.  The mass of the spring-mass-damper system shown below was initially displaced by 1 meter to the right and then released. The subsequent acceleration of the mass was measured using an accelerometer; this data is contained in the file smd_data.txt posted on the class web site. The file contains ascii data which provides the acceleration of the mass as a function of time; the first column of data in the file is time in seconds, the second column is the acceleration in meters/sec². We wish to determine the maximum compressive force experienced by the spring during the time range provided in the data.  The spring force is equal to the spring rate times the displacement,  F_spring = kx.

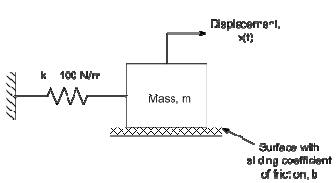
Write a script file which will determine the displacement of the mass as a function of time from the acceleration data.  Trapezoidal integration will provide sufficient accuracy to infer the position and velocity of the seat as a function of time.  Your program should plot the position of the mass as a function of time.  You can use this plot to estimate the maximum negative displacement of the mass; the maximum compressive force is this displacement times the spring rate (k = 100 N/m).

 3.  We wish to numerically perform the following integration: 

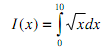
(a) Use Matlab's quad function to perform the above integral.

(b) Analytically evaluate the integral (e.g. do the integration by hand).