Find the hydrostatic force on the bottom of the tank

Reference no: EM131131273

1. Sketch the region bounded by the curves, and visually estimate the location of the centroid. (Do this on paper. Your instructor may ask you to turn in this work.) Then find the exact coordinates of the centroid. (Enter the argument of the logarithmic function in parentheses.)

y = 5/x

y = 0, x = 3, x = 12

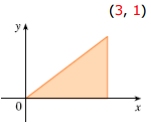
2. Calculate the moments Mx and My and the center of mass of a lamina with density ρ = 7 and the given shape.

3. The masses mi are located at the points Pi. Find the moments Mx and My and the center of mass of the system.

m1 = 6, m2 = 5, m3 = 9;

P1 = (1,5), P2 = (3, -3),P3 = (-2,-2)

4. A trough is filled with a liquid of density 845 kg/m3. The ends of the trough are equilateral triangles with sides 10 m long and vertex at the bottom. Find the hydrostatic force on one end of the trough. (Use 9.8 m/s 2 for the acceleration due to gravity.)

5. Find exact coordinates of the centroid of the region bounded by the given curves.
y = 2sin(3x)
y = 2cos(3x)
x = 0, x = π/12

6. The masses mi are located at the points Pi. Find the moments Mx and My and the center of mass of the system.

m1 = 6, m2 = 5, m3 = 1, m4 = 4;
P1(1, 2), P2(3, 4), P3(3, 7), P4(6, 1)

7. Find the centroid of the region bounded by the given curves. Give your answers correct to two decimal places.
y = x³
x + y = 30
y = 0

8. A swimming pool is 30 ft wide and 60 ft long and its bottom is an inclined plane, the shallow end having a depth of 4 ft and the deep end, 7 ft. Assume the pool is full of water. (Round your answers to the nearest whole number. Recall that the weight density of water is 62.5 lb/ft3.)
(a) Estimate the hydrostatic force on the shallow end.

(b) Estimate the hydrostatic force on the deep end.

(c) Estimate the hydrostatic force on one of the sides.

(d) Estimate the hydrostatic force on the bottom of the pool.

9. A 3 ft high and 5 ft width rectangular plate is submerged vertically in water so that the top is 1 ft below the surface. Express the hydrostatic force against one side of the plate as an integral and evaluate it. (Give your answer correct to the nearest whole number.)

10. Find the exact coordinates of the centroid of the region bounded by the given curves.
x = 8 - y²
x = 0

11. A trapezoidal plate with height h and bases a and 2a is submerged vertically in water as shown. Express the hydrostatic force against one side of the plate as an integral and evaluate it. (Use delta for δ, the weight density constant.)

14. A dam is inclined at an angle of 30° from the vertical and has the shape of an isosceles trapezoid 140 ft wide at the top and 70 ft wide at the bottom and with a slant height of 100 ft. Find the hydrostatic force on the dam when it is full of water. (Round your answer to the nearest whole number. Recall that the weight density of water is 62.5 lb/ft³.)

15. Sketch the region bounded by the curves, and visually estimate the location of the centroid. (Do this on paper. Your instructor may ask you to turn in this work.) Then find the exact coordinates of the centroid.

5x + 6y = 30
x = 0, y = 0

16. Find exact coordinates of the centroid of the region bounded by the given curves.

y = x + 2

y = x²

16. A vertical, irregularly shaped plate is submerged in water. The table shows measurements of its width, taken at the indicated depths. Use Simpson's Rule to estimate the force of the water against the plate. Give your answer correct to the nearest whole number.

Depth (m) 2.0 2.5 3.0 3.5 4.0 4.5 5.0
Plate width (m) 0 0.7 1.8 2.2 2.6 3.3 3.9

17. A tank is 6 m long, 4 m wide, 5 m high, and contains kerosene with density 820 kg/m3 to a depth of 4.5m. (Use 9.8 m/s2 for the acceleration due to gravity.)

(a) Find the hydrostatic pressure on the bottom of the tank.

(b) Find the hydrostatic force on the bottom of the tank.

(c) Find the hydrostatic force on one end of the tank.

18. Pointmasses mi are located on the xaxis as shown. m1 = 25, m2 = 50, and m3 = 10. Find the moment M of the system about the origin and the center of mass x.

19. A large tank is designed with ends in the shape of the region between the curves y = x²/5 and y = 28, measured in feet. Find the hydrostatic force on one end of the tank if it is filled to a depth of 20 ft with gasoline. (Assume the gasoline's density is 42.0 lb/ft3. Round your answer to one decimal place.)

20. An equilateral triangle with sides 3 m is submerged vertically in water so that the base is even with the surface. Express the hydrostatic force against one side of the plate as an integral and evaluate it. (Give your answer correct to the nearest whole number.)

21. A trapezoid with bases 3 m and 7 m is partially submerged vertically in water so that the top is 2 m above the surface and the bottom is 2 m below the surface. Express the hydrostatic force against one side of the plate as an integral and evaluate it. (Give your answer correct to the nearest whole number.)

Reference no: EM131131273

Questions Cloud

Explain the concept behind the installation : Identify the theme for your installation and explain the concept behind the installation. Create a title for your installation

Explain why he made this recommendation : He found that the number of returned planes that had damage to the fuselage was far greater than those that had damage to the engines. His recommendation was to enhance the reinforcement of the engines rather than the fuselages. If damage to the..

Describe the change in dravot and carnehan relationship : Describe the change in Dravot and Carnehan's relationship from the beginning to the end of the story. What is the catalyst for the change and what is the result

How can temperature influence the byproducts of incineration : Describe the impact that temperature changes can have on environmental systems in relation to carbon, nitrogen, and sulfur. How can temperature influence the byproducts of incineration?

Find the hydrostatic force on the bottom of the tank : A tank is 6 m long, 4 m wide, 5 m high, and contains kerosene with density 820 kg/m3 to a depth of 4.5m. (Use 9.8 m/s2 for the acceleration due to gravity.) Find the hydrostatic pressure on the bottom of the tank.

What is the significance of the motif : In Elie Wiesel's memoir, Night, what is the significance of the motif between father/son relationships? How was Elie's relationship with his father important to him? How did his relationship with his father evolve throughout the memoir

What is the story central conflict : Please remember to consider the following questions: What is the story's central conflict? How is the conflict resolved? What do the main character's actions reveal about his or her personality

Describe the different types of mold : describe the different types of mold and their potential health impacts. What are the conditions that promote mold growth?

Valuing stock options the black scholes merton model : Please Solve the all the problems given below on Valuing Stock Options: The Black-Scholes-Merton Model Problem 1 A stock price is currently $40. Assume that the expected return from the stock is 15% and its volatility is 25%. What is the probability ..

User Account

All Pages