Reference no: EM132590306

Math 311 Assignment - Include all the supporting work and justify your answer.

Q1. Which of the following are properties of the error function erf(x) and complementary error function erfc(x)? (Select all that are correct.)

A. erf(0) = 0

B. erfc(0) = 0

C. erf(x) ≥ 0 for x ≥ 0

D. lim_x→∞erf(x) = 1

E. lim_x→∞erfc(x) = 1

F. erf(x) ≥ erfc(x) for x ≥ 0

Include any supporting work with your choices.

Q2. The function f(x) = e^-x, x ≥ 0 is represented by the Sine Fourier Integral as:

f(x) = 2/π ₀∫^+∞αsin(αx)/(1+α²) dα

Evaluate the integral at x = 0 and compare the result with f(0). Explain if/why there is any disagreement in values.

Q2. Submit the solution of only one of the two problems below, as you answer the following questions.

2. a. Use the Laplace Transform to solve the given Boundary-Value Problem (BVP).

2. b. Briefly explain your choice of variable for the Laplace Transform.

2. c. Test the solution found (PDE + I.C. + B.C.).

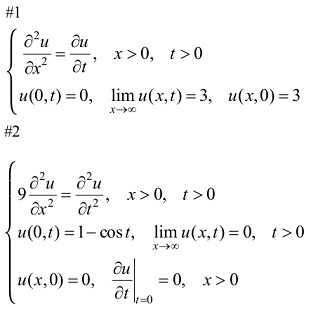
Q3. Submit the solution of only one of the two problems below, as you answer the following questions

3. a. Use a proper Fourier Transform (FT) to solve the given Boundary-Value Problem (BVP).

3. b. Briefly explain your choice of variable used in the FT and the choice of FT itself.

Q4. Discrete Fourier Transform (DFT).

a) Find the Fourier transform of a general signal f = [f1, f2, f3]^T of three values.

b) State the DFT requirements/assumptions related to the measurements above.

c) Find the transform when f = [-3, 0, 5]^T.