Reference no: EM132374945

Question 1 - Laplace transforms

1. Solve the following differential equations using Laplace transforms:

y′′ + y′ - 6y = 15u (x - 2), y (0) = 1, y′(0) = 2.

2. Pesticide applied to the trees has a certain outflow rate to the soil, and at the same time, pesticide in the soil has a certain uptake rate into the trees. Pesticide level in the trees varies with time so repeated applications are required to control the insects. A simplified model obtained from input-output analysis reads

dx/dt = x - 5y + r(t), dy/dt = x - 3y

where x(t) and y(t) are the amounts of pesticide in trees and soil respectively, and r(t) is the amount of pesticide applied to the trees. The independent variable, t represents time in years. In an untreated orchard, the initial data is x(0) = 0, y(0) = 0, since the trees and the soil initially contain no pesticide. A once off application can be modelled in terms of Dirac's δ-function

r(t) = aδ(t),

where a is the amount of pesticide (in kg) applied to the trees. Answer the following questions assuming that 4 kg of pesticide were applied.

(a) Using Laplace transforms find solutions for x(t) and y(t).

(b) The pesticide remains effective as long as its amount in the trees is above 1 kg. Estimate the time when the pesticide needs to be applied again to remain effective.

Hints: the answer is time t, such that x(t) = 1. To find t you need to solve the equation x(t) = 1. The analytical solution might be too difficult to find. So you can use Maple or any numerical method for finding the solution approximately. Make sure the answer is expressed in years and months.

(c) Explain, in words a farmer can understand, the above mathematical results.

Question 2 - Fourier Series

1. Find the Fourier series for the function below that has a period of 2π

f(x) = x² - x, - π ≤ x ≤  π.

2. Sketch on the same axis, f(x) and the partial sum of the Fourier series determined in part 1, up to n = 3. The domain of the sketch to be plotted is - π ≤ x ≤  π. The sketch may be computer generated or hand drawn.

3. Use the above Fourier series to determine the sums:

_n=1Σ^∞ (-1)ⁿ/n²

Hint: use a particular value of x such that the Fourier series found in part 1 takes the required form.

Question 3 - Fourier (Sine/Cosine) Transform

1. Find the Fourier transform of

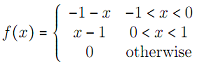
2. Find the Fourier cosine transform of

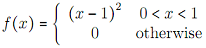
Question 4 - Partial differential equations

1. Check whether the function

u (t, x) = arc tan (t/x) + cos (t² + x²)

is a solution of the differential equation

xu_t - tu_x = 1.

2. Use separation of variables to find a solution of the equation

x²u_t - tu_x = 0.