Reference no: EM133067645
Assignment: Process Modeling and Simulation
Question 1. The exothermic reaction A→B takes place in a jacketed CSTR. The dynamic model of the reactor is given below.
VdcA/dt = q(cAi - CA) - VkcA k = k0e-E/RT
VρCdT/dt = wC(Ti - T) + (-ΔHR)VkcA + UA(Tc - T)
|
q=100
|
CAi=1
|
V=100
|
C=0.239
|
ρ=1000
|
ΔHR=-5×104
|
|
E/R=8750
|
K0=7.2×1010
|
UA=5×104
|
T(0)=Ti=350
|
Tc=305
|
CA(0)=0.5
|
a) Simulate the above process until t=20 using the forward Euler method with a fixed step size of h=0.1. Plots the solution (concentration and temperature profiles). Is the solution stable?
b) Using the eigenvalue technique discussed in the class, find out if the process is stable. Also, try to find the maximum step size for which the forward Euler method is stable for this process. Use the initial conditions at the linearization point.
c) Repeat Part (a) with half of the maximum step size obtained above and plot the solution. Is the solution stable now? If not, comment on the possible reason(s).
d) Now, simulate the process using ode15s with the 'BDF' option 'on', and absolute and relative tolerances of 10-6 and 10-3, respectively. Plot the solution. Is it stable now?
e) For comparison, plot on the same figure the profiles obtained in Part (d) together with those obtained from the forward Euler method with a stabilizing step size of your choice. Comment on the accuracy of forward Euler.
f) Try to find a step size that would make forward Euler as accurate as the BDF method in ode15s (or at least close enough). Compare the computational times of both solvers when their solutions are satisfactorily close.
g) (Bonus) Simulate the process with the user-supplied Jacobian option of ode15s enabled. Provide the Jacobian matrix using automatic differentiation (use ADiMat for example). Compare the results in terms of computational time and number of function evaluations
with and without using the user-supplied Jacobian (see the odeset option Stats). Plot solution profiles from both cases on the same figure.
Question 2. Consider the large-scale model x·i (t) = λx2i(t), i = 1, ........ n expressed as

where λ = -104 and n = 5000. All the state variables start from 1.
a) Simulate the system with ode15s until t=1 with and without a user-supplied Jacobian (the analytical Jacobian matrix is easily obtained in this case). Leave other solver options to default. Compare the two simulations in terms of computational time and number of function evaluations. Which case is solved more efficiently and why?
b) Now, solve the system using ode45 using the default options. Compare the number of steps and computational time with those from ode15s. Explain possible reasons for the difference if it is significant.
Question 3. The dynamic model of two constant-volume CSTRs in series with the reaction A→B is given below. It is desired to have a cyclic steady state for the concentration of the product B exiting the second CSTR. You are asked to find the right profile for the inlet concentration to make that happen.
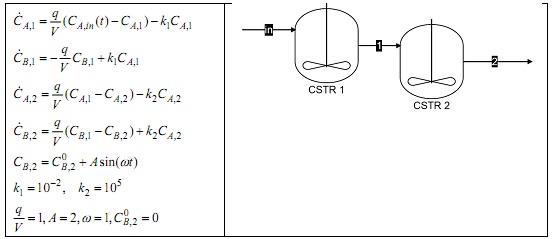
a) Find the form and index of the DAE model using the Pantelides approach.
b) Form the system of consistent initialization, and find degrees of freedom for initialization using the Pantelides approach.
c) Solve the initialization problem (e.g., using fsolve), and report initial conditions for all the state variables and their derivatives, if applicable.
d) Can the model be simulated as is? Try it out. Use the initial conditions calculated in the previous part.
e) Convert the model to an explicit ODE system and solve it using ode15s. For the state variables, use the initial conditions calculated in Part (c). Plot all the state variables. Does the solution exhibit the desired cyclic behavior for CB,2? If not, why?
f) Now, use Gear's method to stabilize the constraints that have been lost during the index reduction procedure. Write the resulting index-2 DAE system.
g) Simulate the process again with the constraints stabilized. Plot all the state variables. Does the solution exhibit the desired cyclic behavior for CB,2 this time?