Reference no: EM13799760

1. (a) A horizontal long straight wire carries a current of I₁ = 8 A from left to right. The wire is tangential to a circular loop of wire of radius R = 0.03 m lying immediately below it. The loop carries a current of I₂ = 2 A in the counter-clockwise direction. Assuming that the thicknesses of the wires are negligible, find the magnitude and direction of the net magnetic field at the centre of the circular loop?

(b) A second long wire, also carrying a current I₁ = 8 A from left to right, is added and lies parallel to the first wire, tangential to the loop but immediately below the loop. Find the magnitude and direction of the net magnetic field at the centre of the circular loop.

(c) Find the magnitude and direction of the net magnetic field at the centre of the circular loop if the direction of the current I₁ = 8 A in the second wire lying below the loop is reversed so that it flows from right to left.

(d) Find the magnitude and direction of the net magnetic field at a point midway between the two horizontal wires if the circular loop is removed and each of the wires carries a current I₁ = 8 A from left to right. The two wires are, as before, 0.03 m from each other.

2. The following (Kirchhoff's) equations describe an electric circuit:

-I­₁ (220) + 5.80 - I₂ (370) = 0

+I₂ (370) +I₃ (150) - 3.10 = 0

+l₁ + I₃ - I₂ = 0                                    

Obviously, the numbers 220, 370 & 150 refer to values of resistances, 5.80 & 3.10 refer to emf values and I₁,I₂ &I₃ refer to currents.

(a) Draw a diagram of the circuit and clearly label the component parts, using R₁, R₂ & R₃ for resistances, E₁ & E₂ for emf devices and I₁,I₂ & I₃ for the currents in the appropriate loops.

(b) Calculate the unknown currents and clearly specify their directions.

3. A charged particle, passing through a certain region of space, has a velocity whose magnitude and direction remain constant.

(a) If it is known that the external magnetic field is zero everywhere in this region, can you conclude that the external electric field is also zero? Explain clearly.

(b) If, on the contrary, it is known that the external electric field is zero everywhere in this region, can you conclude that the external magnetic field is also zero? Explain clearly.

4. An electron is moving in a region in which both an electric field and a magnetic field are present. It obviously experiences a total force due to the two fields given by F = q E + q (v x B). The electron has an initial velocity of (12 j + 15 k) km/s and a constant acceleration of (2 x 10¹² i) m/s². If B = (400 x 10^-6 i) Tesla, Find the electric filed E in vector form. Note that the quantities in bold are vectors.

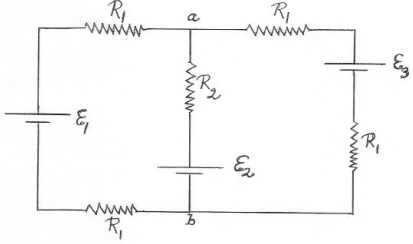
5. (a) Find the three currents in the circuit shown below.

(b) Find the potential difference between the points a and b in the circuit. Which point is at a higher potential?

Assume that R₁ = 1.0 Ω, R₂ = 2 Ω, ε₁ = 2 V and ε₂ = ε₃ = 4 V

6. Consider the series RC circuit shown below with R = 10⁶ Ω, ε = 30 V and C = 5 µF.

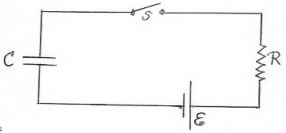
(a) Find the time constant of the circuit.

(b) Find the maximum charge on the capacitor after the switch is thrown closed.

(c) Find the current in the resistor 10 s after the switch is closed.

7. (a) What current is needed in a 2 cm diameter coil to cancel the earth's magnetic field (B = 5 x 10^-5 T) at the centre of the coil?

(b) Can a constant magnetic field set into motion an electron initially at rest? Explain your answer.

8. (a) A current of 0.09 A flows through a square coil of wire of side 1.414 x 10^-2 m consisting of 50 loops. The coil is placed in a magnetic field of 0.3 T. Find the magnetic moment µ of the coil and the maximum torque that the magnetic field can exert on the coil.

(b) A particle with a charge -q is moving from right to left (east to west) with a velocity v in a region where a uniform magnetic field B is directed perpendicular to the paper and coming out towards the reader. How should electric field E should be directed so that the force it applies to the particle can balance the magnetic force the particle experiences due to B?

9. In the circuit shown below, determine

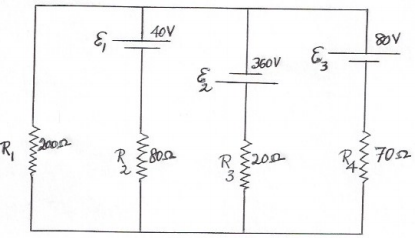
(a) The current in each resistor and indicate the direction in which it flows, and

(b) The potential difference across the 200 Ω resistors.

10. In a repetition of J. J. Thomson's experiment (which led to the discovery of the electron) an accelerating potential of 250 V and a deflecting electric field of magnitude 6 x 10⁶ N/C are used.

(a) At what speed do the electrons travel?

(b) What magnitude of magnetic field will you need so that the electrons pass undeflected?

(c) With this magnetic field, what will happen if you decrease the accelerating potential below 250 V?