Reference no: EM132449433
Problems -
Problem One: An annulus (a disk with a hole) has an outer radius R and an inner radius R/2. An amount Q of electric charge is uniformly distributed over the shaded area.
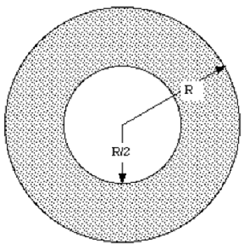
(a) Find the potential as a function of the distance on the axis of the annulus.
(b) Find the electric field on the axis of the annulus.
Problem Two: Consider a non-conducting rod of length l having a uniform charge density λ.
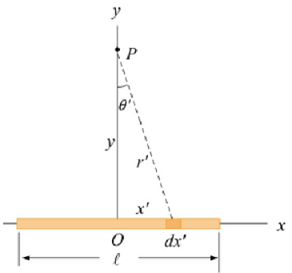
(a) Find the electric potential at P, a perpendicular distance y above the midpoint of the rod.
(b) Find the corresponding electric field.
Problem Three: A thin rod extends along the z-axis from z = -d to z = d. The rod carries a positive charge uniformly distributed along its length with charge density λ = Q/2d.
(a) Calculate the electric potential at a point z > d along the z-axis.
(b) What is the change in potential energy if an electron moves from z = 4d to z = 3d?
(c) If the electron started out at rest at the point z = 4d, what is its velocity at z = 3d?
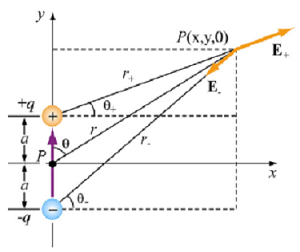
Problem Four: Consider an electric dipole along the y-axis, as shown in the figure below. Find the electric potential V at a point P in the x-y plane, and use V to derive the corresponding electric field.