Reference no: EM131702897

SECTION - A

All parts for this question are compulsory

a) Find the 5^th derivative of e^xx³ .

b) Find the stationary point of f(x,y) = 5x² + 10y² + 12xy - 4x - 6y + 1

c) If u= x²-y² + sin yz where y = e^x and z= log x find du/dx

d) If x = r cosθ, y = r sinθ show that ∂(x,y)/∂(r,θ) = r

e) Reduce the matrix 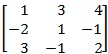into normal form.

f) Prove that the matrix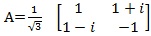 is unitary.

g) Change the order of integration in the double integral ₀∫^∞_x∫^∞ e^-y/y dxdy and hence find its value.

h) Evaluate the following double integrals ₀∫¹₀∫^_√(1+x2₎ dxdy/(1+ x² +y²)

i) Find the value of m if F^→ = mxi^{^}- 5yj^{^}+ 2zk^{^} is a solenoidal vector.

j) Find the unit normal at the surface z = x² + y² at the point (1,2,5).

SECTION - B

Attempt any three parts of the following

a) If y = a cos (log x) + b sin(log x) then prove that x²y₂ + xy₁ + x = 0 and x²y_n+2 + (2n+1) xy_n+1 + (n²+1)y_n = 0.

b) Prove that ∂(u,v)/∂(x,y) .∂(x,y)/∂(u,v) =1

c) Find the Eigen values and Eigen vectors of the following matrix :

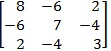
d) To prove the Legendre's duplication formula Γn Γ(n+1/2) = √π/2^2n-1.Γ(2n)

e) Verify Gauss's divergence theorem for the function

F^→ = x²i^{^} + y²j^{^}+ z²k^{^} taken over the cube 0 ≤ x, y, z ≤ 1.

SECTION - C

Attempt any two parts from each question.

All questions are compulsory.

1. a). Find the nth derivative of 1/(x² - 5x + 6) .

b). State and prove Euler's theorem for homogeneous functions.

c). If y = [ x + √(1+x²)]^m then find (y_n)₀.

2. a). If u₁ = (x₂x₃)/x₁, u₂ = (x₃x₁)/x₂, u₃ = (x₁x₂)/x₃ Prove that J(u₁u₂u₃) = 4.

b). The period of a simple pendulum is T = 2π√(l⁄g) Find the maximum error in T due to possible errors up to 1% in l and 2.5% in g.

c). In a plane triangle ABC find the maximum value of u = cos?A cos?B cos?C.

3 a). Find the inverse of 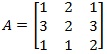by elementary operations.

b). Test for consistency of the equations

2x - 3y + 7z = 5
3x + y - 3z = 13
2x + 19y - 47z = 32.

c). Show that the system of three vector

(1,3,2), (1,-7,-8), (2,1,-1) of V₃ (R) is linearly dependent.

4 a). Evaluate the integral ?e^x+y+z dx dy dz taken over the positive octant such that x + y + z ≤ 1 with the help of Liouvllis Theorem.

b). Show that ₀∫²(8 - x³)^-1/3 dx = 2π/(3√3).

c). Evaluate ?y dx dy over the area between the parabolas y² = 4x and x² = 4y.

5 a). Show that the vector field F^→ = yzi^{^} + zx+1j^{^} + xy k^{^} is conservative field its scalar potential. Also find the work done by F^→ in moving a particle from (1,0,0) to (2,1,4).

b). Prove that Div (? a ¯ )= ? Div a ¯ + (grad ?).a ¯.

c). Find the directional derivative of ? = 5x²y - 5y²x + 5/2z²x at the Point (1,1,1) in the direction of line (x-1)/2 = (y-3)/(-2) = z/1.