Reference no: EM133042584

UNIT 28 Further Mathematics for Construction - Higher National Certificate/Diploma in Construction and the Built Environment

Scenario:

You are working as an Engineering Research Technician in a research and development laboratory where good analytical skills and understanding of mathematics is essential for everyday work. Your line manager has informed you that you need to improve and update your present Mathematical skills to work effectively & contribute to the research team. The essential skills include Number theory, Matrices, graphical and numerical methods, Models of engineering systems using ordinary differential equations .

To test your suitability for this position in research, the following tasks have been compiled for you to complete.

Learning Outcome 1: Apply instances of number theory in practical construction situations.

Task 1
a. Convert each number into denary,

• 11001.01

• 4D

b. calculate the following in both binary and denary

•11001+1001

Task 2
Apply de'Moivre's theorem or otherwise to solve for Zo and C from these expressions given below :
Z0=Z/Y and C=Z*Y
Where:
• Z is a complex number.
• Y is also a complex number.
• Re (Z0) >0 and Re (C) >0
Find Z0 and C when:
Z = 1 + 5 j,Y = 1 - 3 j

Task 3

a. Simplify the following equation:
G = 1 x e j^2Π x 2 x e^j0.5 x 0.5x e ^j0.75

b. Express the following expression in complex exponential form:

v=20sin (1000t-30°)

Task 4

Find a formula for cos (3θ) in terms of cos (θ) and sin (θ) using de Moivre's Theorem.

Learning Outcome 2: Solve systems of linear equations relevant to construction applications using matrix methods

Task 1

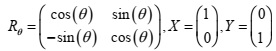
a) Determine the vector Z when θ = Π/2, Z = R_θ x ( X - Y )

b) Determine the determinant of the matrix R_θ when θ = Π/4

c) Determine the inverse of R_θ When θ = Π/4

d) Solve the following equation for

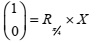
Task 2

You have been asked by the structural engineering department to find the determinant and inverse of the following matrix

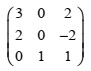
Task 4
You have been asked to the following set of equations that have been obtained from the structural engineering Department and verify your calculations using computer methods
2x₂ + x₃ = -8
x₁ - 2x₂ - x₃ = 0
- x₁ + x₂ + 2x₃ = 3

Learning Outcome 3: Approximate solutions of contextualised examples with graphical and numerical methods

Assignment Brief and Guidance

Task 1
The engineering department has developed the following equation for the bending moment of a beam and you have asked to investigate its behaviour
M ( x) = x³ - 3x² - 4
The Beam is 4m long and the design team suspect the is problem if the bending moment is zero in the range between 3-4m and you have been asked to
a) Plot the bending moment at 0.5m interval for the range 0 ≤ x ≤ 4m 0 ≤ x ≤ 4 and determine if the bending moment is zero in range 3m ≤ x ≤ 4m
b) Use the graph to estimate where the bending moment is zero
c) Use the bisection method to numerically estimate the exact location where the bending moment is zero
d) Newton-Raphson method to obtain the required location
e) Compare the results of the above method to determine which gives a best solution

Task 2
The following offsets are taken from a chain line to an irregular boundary towards right side of the chain line.

chainage          0         25     50     75     100      125      150

Offset 'm'       3.6       5.0       6.5       5.5       7.3       6.0       4.0

Common distance d =25m
You have been asked to estimate the area using the following methods and compare and comment on their difference and accuracy.
a) Trapezium Rule
b) Simpson's Rule

Task 3
The equation governing a body travelling in a water channel is given by the following equation
dv/dt = 1 - v²

Plot the velocity time graph for the object and determine the final velocity and the time taken to reach this velocity

Learning Outcome 4: Review models of construction systems using ordinary differential equations

Assignment Brief and Guidance

TASK 1

The equation of catenary is given by the following second order differential equation
y " = 5
x = 0, y = 100
x = 100, y = 100

Solve the above differential equation and plot the curve at 10m intervals.

Task 2
The differential equation governing the motion of a particle is given by the following differential equation
y ''+ 5 y = 0
t = 0, y = 20
Solve the above and plot the results and determine the amplitude and frequency of the oscillations

Task 3
A new series of tests is carried out and the equation modified to
y ''+ 2 y + 5 = 0
y = 20, t = 0

Use Laplace transforms or any other method to solve the new equations and plot the function and comment on the results.

Attachment:- Further Mathematics for Construction.rar