Reference no: EM13311584

Question 1. Five office cubicles are arranged in the following pattern:

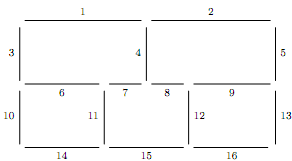
As indicated, 16 cubicle partitions are used to build the cubicles. An enthusiastic network cabler wishes to install a single long cable so that it passes through every partition exactly once. Is this possible? Either indicate how it may be done, or prove that it is impossible. (The small gaps in the picture are just for illustrative purposes, and cannot be used for the cable.)

Question 2. A simple graph G has 7 vertices and 9 edges. The degrees of some of its vertices are 2, 2, 4, 2. Furthermore, G is known to have an Euler circuit.

Find the degrees of the remaining vertices, and draw a picture of G.

Question 3. Pierre can choose between two dice games. Both use (unbiased) six-sided dice. In game A, Pierre throws one die four times. He wins if at least once he rolls a six: .

In game B, he has 24 turns, and each time he throws two dice simultaneously. This times he wins if he rolls at least one \double six": .

(a) Which game is Pierre more likely to win?

(b) Is the following argument correct? Explain:

A double six in a single turn in game B is 1/6 as likely as rolling a six in one turn in game A. But there are 6 times as many turns in game B as game A. Thus the two games are equally good bets.

Question 4. 7 people are attending a concert.

(a) In how many dierent ways can they be seated in a row?
(b) Two attendees are Alice and Bob. What is the probability that Alice sits next to Bob?
(c) Bob decides to make Alice a rainbow necklace with 7 beads, each painted a dierent colour on one side (red, orange, yellow, blue, green, indigo, violet), placed on a chain that is then closed to form a circle. How many dierent necklaces can he make? (Since the beads can slide along the chain, the necklace with beads ROYGBIV would be considered the same as OYGBIVR for example. The beads are plain on the back, so the necklace cannot be turned over.)