Reference no: EM131035156

I need the answers for all problems with the explanation for each solution.

Problem 1 Response Time of a Phase Modulator

A GaAs crystal with refractive index n = 3.6 and electro-optic coefficient r = 1.6 pm/v is used as an electro-optic phase modulator operating at λ_o = 1.3 μm in the longitudinal configuration.

The crystal is 3 cm long and has a 1 cm² cross-sectional area. Determine the half- wave voltage V_Π, the transit time of light through the crystal, and the electric capacitance of the device (the low-frequency dielectric constant of GaAs is ∈/∈_o = 13.5). The voltage is applied using a source with 50 Ω resistance. Which factor limits the speed of the device, the transit time of the light through the crystal or the response time of the electric circuit?

Problem 2 Microwaved Acousto Optics

One end of a lithium niobate (LiNb0₃) crystal is placed inside a microwave cavity with an electromagnetic field at 3 GHz. As a result of the piezoelectric effect (the electric field creating a strain in the material), an acoustic wave is launched. Light from a He-Ne laser (λ_o = 633 nm) is reflected from the acoustic wave. The refractive index is n = 2.3 and the velocity of sound is v_s = 7.4 km/s. Determine the Bragg angle. Since lithium niobate is also an electro-optic material, the applied electric field modulates the refractive index, which in turn modulates the phase of the incident light. Sketch the spectrum of the reflected light. If the microwave electric field is a pulse of short duration, sketch the spectrum of the reflected light at different times indicating the contributions of the electro-optic and acousto-optic effects.

Problem 3 Sensitivity of an Electro Optic Modulator

Sensitivity of an Interferometric Electro-Optic Intensity Modulator. An integrated-optic intensity modulator using the Mach-Zehnder configuration, illustrated below, is used as a linear analog modulator. If the half-wave voltage is V_Π = 10 V, what is the sensitivity of the device (the incremental change of the intensity transmittance per unit incremental change of the applied voltage)?

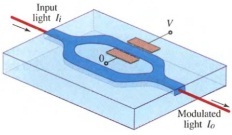
Problem 4 Electro Optic Switch

You are asked to design a transverse electro optic switch using LiTaO₃ for a TE propagating wave. The physical configuration for the switch is show in the Figure 1.

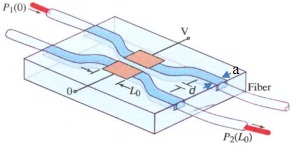
Figure 1 Electro Optic Switch Layout

The material characteristics for LiTaO₃ are given Table 1.

Table 1 Material Characteristics of LiTaO₃

The system is configured for transverse operation. The TE transverse field distribution of the wave in the first channel, u_m(y), in the slab is given by:

                cos(2Π.(sinθm/λ).y),   m = 0, 2, 4,.....

u_m(y) ∝                                                          -0 ≤ y ≤ a

               sin(2Π.(sinθm/λ).y),     m = 1, 3, 5,.....

               exp(-y_my),   y > a

u_m(y) ∝

               exp(y_my),    y < 0

1. Derive an expression for the coefficients for the wave entering the switch for each term of u_m(y). Circle all major solutions during your analysis. Determine the confinement factor for the wave if a = 0.5 μm and d = 1 μm for λ_o = 632.8 nm. Assume both waveguides are operating at an m = 0 condition.

2. Find the Coupling Coefficient between the two channels. Assume that the channels are of the same index. Recall that the coupling coeffients are found by

C₂₁ = 1/2 (n₂² -n²)k_o²/β₁ ^a∫_a+d u₁(y)u₂(y)dy,

C₁₂ = 1/2 (n₁² -n²)k_o²/β₂ ^-a∫_-a-d u₂(y)u₁(y)dy,

3. Determine the length of the waveguides so that the device acts like a 3 dB coupler.

4. The transmission through channel two is described by

Τ = Π²/4 sinc²[1/2√(1 + 3(v/vo)²)]

where

V₀ = √3.d/L₀.λ_o/2n³r = √3/Π.Cλ_od/n³r

What is the voltage necessary to switch from channel one to channel two. Find the value of V_o.

5. What is the sensitivity of the Vo with respect to the distance between the channels.

Problem 5 Coupling Light from an LED into an Optical Fiber

Calculate the fraction of optical power emitted from an LED that is accepted by a step-index optical fiber of numerical aperture NA = 0.1 in air and core refractive index 1.46. Assume that the LED has a planar surface, a refractive index n = 3.6, and an angular dependence of optical power that is proportional to cos⁴(θ). Assume further that the LED is bonded to the core of the fiber and that the emission area is smaller than the fiber core.