Reference no: EM131076147

MATH 54 QUIZ 6-

1. Is λ = 1 an eigenvalue of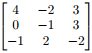? If so, find one corresponding eigenvector.

2. Find a basis for the eigenspace corresponding to each listed eigenvalue: A =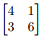, λ = 3, 7.

3. Find the characteristic polynomial of the following matrix.

4. Diagonablize the following matrix, if possible. It has eigenvalues λ = 2, 3.

5. Let B = {b₁, b₂, b₃} be a basis for a vector space V and let T: V → R² be a linear transformation with the property that

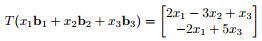
Find the matrix for T relative to B and the standard basis for R².

6. True/False (no justification required, full credit only if all 4 parts are correct)

(i) A is diagonalizable if A has n eigenvectors.

(ii) If A is diagonalizable, then A has n distinct eigenvalues.

(iii) If AP = PD, with D diagonal, then the nonzero columns of P must be eigenvectors of A.

(iv) If A is invertible, then A is diagonalizable.