Reference no: EM13829852
1 - Assume the following is given across a resistive load.
v(t) = Acos(θ)
i(t)=Bcos(θ)
a) Find the average of the voltage and current for 0 ≤ θ ≤ 2Π.
b) Find the average power and show that (v(t))(i(t)) # P in general.
c) Find the rms component of the voltage. How does Vrms relate to P?
d) An inductor is added. Now the load is an RL load. Find the average power across the load.
2- For the following waveform
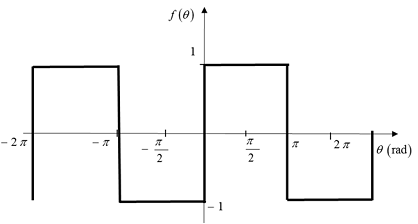
a) Find the Fourier series coefficients an, bn and a0.
b) Write a MATLAB function that accepts an, bn, a0, θ, and n (number of harmonics) and outputs the function. The function form should be similar to function fth = fourier_series(a0,an,bn,n,theta)
c) Use the function you wrote to plot f (θ) vs θ for n=1, n=1:1:5 and n=1:2:5 and n=1:1:30. Which plot gives the closest resemblance to the original waveform shown above.
d) Plot the harmonic spectrum of f (θ) . (i.e.: an vs n and bn vs. n )
3- Prove that the average current across a capacitor is equal to zero.