Reference no: EM133029134

Assignment -

Q1. Two springs each have spring constant k and equilibrium length l. They are both stretched a distance l and attached to a mass m and two walls, as shown in figure below. At a given instant, the right spring constant is somehow magically changed to 3k (the relaxed length remains l). What is the resulting x(t)? Take the initial position to be x = 0.

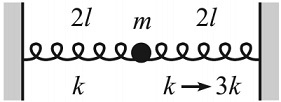
Q2. (a) Two vibrations are given by: x₁ = A cos(ω₁t + φ₁) and x₂ = A cos(ω₂t + φ₂). Find an expression for their superposed motion in the form a cos(bt + c) cos(dt + e) and determine the constants a through e in terms of the given parameters. Use complex notation in your derivation, as in the class notes.

(b) Consider the vibrations x₁ = 3 cos(3t + π/5) and x₂ = 4 cos(4t + π/8). What is the expected period for x₁ + x₂?

(c) Complex number and phasor practice: Express the following in the form z = Re[Ae^i(ωt+α)] and sketch them by hand or plot them in pylab in the complex plane at t = π/ω (i.e. at one half period):

z = 5 sin ωt + 6 cos ωt;

z = sin(ωt + π/3) - cos ωt;

z = sin ωt + 2 cos(ωt + π/6) + cos ωt.

Q3. A mass m connected to an ideal spring slides frictionlessly on a surface. It is connected to a "dashpot" damper that produces a resistive force proportional to the velocity v of the mass.

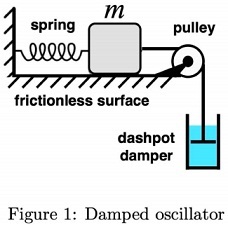
We did some experiments on this device and made the following observations:

If the block is pushed horizontally to the left with a static force equal to mg, the spring compresses a distance h.

If the block is moved at a steady speed U = 3√(gh), the dashpot damper produces a resistive force of magnitude mg.

Now the system is displaced and released from rest, setting it into oscillation.

(a) Find the angular frequency of the underdamped oscillations of the system, expressed as a multiple of √(g/h).

(b) After what time, expressed as a multiple of √(h/g), is the amplitude of the underdamped motion decreased by a factor of e from its initial displacement?

Q4. Consider a particle of mass m, free to move in one dimension x, which is subjected to a drag force -by = -bx but no spring-like restoring force. The particle is initially at rest, so x₀ = x(0) = 0 and v₀ = x(0) = 0. At t = 0 we suddenly begin to apply a driving force f(t) = mA cos(ωt) to the particle, where A > 0 is a constant.

For t > 0, the particle exhibits some transient motion but after a long time it settles down into a regular steady-state oscillation.

(a) Write down F = ma for this system and show that the transient part x_t(t) of the total displacement x(t) of the particle is given by

x_t(t) = C + (D/β)e^-βt, (1)

where β = b/m and C and D are constants to be determined later from the initial conditions.

(b) We learned in class that the long term, or steady state, part of the motion is found from the particular solution x_p(t) of the forced equation of motion.

Find a particular solution by "complexifying" the equation of motion by assuming a complex applied force f^~(t) = mAe^iωt, so that f = R[f^~], where R[·] means "take the real part". Using a clever guess, find a complex expression x^~_p(t) for the long-term, steady-state motion.

(c) By taking the real part of the complex expression you found in the previous part, find the real steady state motion x_p(t) = R[x^~_p(t)]. Write it in the following form

x_p(t) = B cos(ωt + φ), (2)

finding expressions for the real amplitude B and phase φ.

(d) Finally, combine the real transient and the steady-state motion to get the full motion for all time, x(t) = x_t(t) + x_p(t). Apply the initial conditions and determine the constants C and D. You may assume the result of the previous part and just write them in terms of B and φ.