Reference no: EM132321524

Mathematics for Construction Assignment -

Purpose of this assignment -

1. Identify the relevance of mathematical methods to a variety of conceptualized construction examples.

2. Investigate applications of statistical techniques to interpret, organize and present data by using appropriate computer software package.

3. Use analytical and computational methods for solving problems by relating sinusoidal wave and vector functions to their respective construction applications.

4. Illustrate the wide-ranging uses of calculus within different construction disciplines by solving problems of differential and integral calculus.

Task 1 -

Task 1.1 -

Scenario: An unnamed island in polar region is approximately 50,000 mile², 75 percent of which is covered by ice with an average thickness of 1300 meters. Estimate the mass of the ice in this island (assume two significant figures). The density of ice is 0.917 g/mL (1cm³ = 1mL)

i. Clearly specify the units (dimensions) of the desired product.

ii. Specify all known values with their associated units.

iii. Specify relevant formulas and all conversion factors.

iv. Develop an equation such that the units of the left side are equivalent to the units of the right side.

v. Perform the calculation.

Scenario: Dimensions of some common mechanical quantities

M ≡ mass, L ≡ length, T ≡ time

Quantity	Dimension	MKS unit
Angle	dimensionless1	Dimensionless = radian
Steradian	dimensionless	Dimensionless = radian2
Area	L2	m2
Volume	L3	m3
Frequency	T-1	s-1 = hertz = Hz
Velocity	L · T-1	m · s-1
Acceleration	L · T-2	m · s-2
Angular Velocity	T-1	rad · s-1
Angular Acceleration	T-2	rad · s-2
Density	M · L-3	kg · m-3
Momentum	M · L · T-1	kg · m · s-1
Angular Momentum	M · L2 · T-1	kg · m2 · s-1
Force	M · L · T-2	kg · m · s-2 = newton = N
Work, Energy	M · L2 · T-2	kg · m2 · s-2 = joule = J
Torque	M · L2 · T-2	kg · m2 · s-2
Power	M · L2 · T-3	kg · m2 · s-3 = watt = W
Pressure	M · L-1 · T-2	kg · m-1 · s-2 = pascal = Pa

A constant force of magnitude F acts over a distance d on an object of mass m. Find the final speed v of the body.

vi. List the quantities that might be involved to calculate the speed v and propose a generic equation.

vii. Using a dimensional analysis on both left and right-hand side and follow the algebraic relations.

viii. Derive the equation of final speed v.

Task 1.2 -

i. What is arithmetic progression.

ii. Write down the general expression for n'th term of an arithmetic progression.

iii. Determine the 8^th term of a series 2, 7, 12, 17 ....

iv. What is geometric progression?

v. Write down the general expression for n'th term of a geometric progression.

vi. A drilling machine is to have 6 speeds ranging from 30 rev/min to 960 rev/min. If the speed form a geometric progression, determine the value of each speed.

Task 1.3 -

 i. RC Discharge

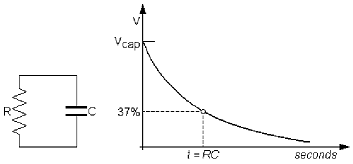
When a capacitor C discharge through a resistor R the voltage V at any time t after the start is related to time t by V = 12 e^-t/RC Volts. Make t the subject of the formula. Given RC = 2 seconds, evaluate the time when V = 6 Volts.

ii.

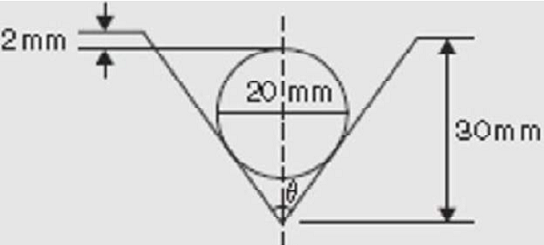
The angle of a tapered groove is checked using a 20mm diameter roller shown above. If the roller lies 2mm below the top of the groove, determine the value of angle θ.

iii.

A chain hangs in the form give by y = 40 ch (x/40). Determine, correct to 4 significant figures,

(a) The value of y when x is 30.

(b) The value of x when y = 50.

Task 2 -

Task 2.1 -

Scenario: A sample of five tests was taken determine the unconfined compression strength (in tons/foot²) of soil, with the test results shown in table below:

Soil strength of sampled soil
Sample number	Strength of tested soil (Tons/ foot2)
1	2.8
2	3.5
3	6.9
4	4.6
5	4.3

i. Calculate the mean of samples.

ii. Calculate the variance and standard deviation of those samples.

iii. Use coefficient of variation to determine the safety of the soil when it is used in a construction site.

Scenario: This is the simplest control chart.

Sample size = the number of selected sample from a batch = k

Number of measurements on each sample test = n

After computing the mean of the k x n measurement values (µ) and standard deviation (σ), the upper and lower control limits for quality control can be determined by

LCL_x^- = µ - 3σ/√n and UCL_x^- = µ + 3σ/√n

Quality control on the IC chip by measuring the output voltage using 3 σ control chart.

5 samples randomly picked up from a storage bin with IC chip mass produced from a process.

3 measurements of voltage output (mV) from each sample, recorded as follows

iv. Calculate the mean of k x n measurement values (µ) and standard deviation (σ).

v. Calculate the upper and lower control limits for quality control.

vi. Draw the quality control chart and explain how to use the chart to control manufacturing process.

Task 2.1 -

Analyze the probability distributions for discrete and continuous data with the following situations.

i. Concrete blocks are tested and it is found that, on average, 7% fail to meet the required specification. To pick up 9 concrete blocks from a batch of concrete blocks in a construction site, determine the probabilities that less than three blocks out from the chosen 9 concrete blocks will fail to meet the specification.

ii. A construction company wants to recruit a technical assistant to work in a new site and the offered salary is HK$11,500. Current research has indicated that the average monthly income for a technical assistant in construction industry in above 13K Hong Kong dollars. It is also known income is shown in Table 2.2. Use the sample data from the table to predict whether the construction company is able to recruit the assistant? Use the level of confidence to support your claim on this recruitment matter.

a) Use z value to predict the chance of hiring a technical assistant using an offered salary of HK$11,500.

b) Applying the z value theorem, determine how much monthly income would be able to recruit a new technical assistance, by the construction company, to work in the new site with a change of 90% successful.

The formula for find the z value is given as follows:

z = (X^- - μ)/(σ/√N)

where μ is the population mean, σ is the population standard deviation, and N is the sample size.

x^- is sample mean

The z value table of normal sampling distribution is shown in Appendix I.

Table 2.2 Sample of monthly income of technical assistance
13800	16500	18500
12500	12000	11800
11200	9800	14500
14300	11800	16500
10050	13600	11500
12800	15500	10900
9600	13900	10800
8900	20000	15000
11300	11600	11800
12800	13500	12800

Scenario: Population mean of IQ = 100, population standard deviation = 16

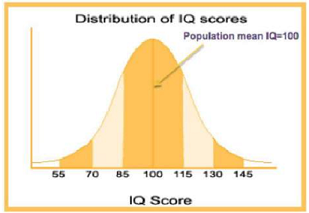
The IQ of some people were sampled and measured.

The hypothesis was that the mean IQ of those measured samples was significantly higher than the population mean.

The sample measurement was below:

Sample size N = 16

Sample mean IQ = 108

In social science, typically 5% probability of Type 1 error is acceptable.

iii. Describe Type I and Type II error in significant test.

iv. Calculate the z value.

v. Find the probability p value from the z value table.

vi. Interpret the statistical result and comment on the hypothesis.

Task 3 -

Task 3.1 -

Scenario: A support beam, within an industrial building, is subjected to vibrations along its length; emanating from two machines situated at opposite ends of the beam. The displacement caused by the vibrations can be modelled by the following equations,

x₁ = 3.75 sin (100 πt + 2π/9) mm

x₂ = 4.42 sin (100 πt - 2π/5) mm

i. State the amplitude, phase, frequency and periodic time of each of these waves.

ii. When both machines are switch on, how many seconds does it take for each machine to produce its maximum displacement?

iii. At what time does each vibration first reach a displacement of -2mm?

iv. Use the compound angle formulae to expand x₁ and x₂ into the form A sin100 πt ± B cos100πt, where A and B are numbers to be found.

v. Using your answers from part iv, express x₁ + x₂ in a similar form. Convert this expression into the equivalent form R sin (100 πt + α).

vi. Using appropriate spread sheet software, copy and complete the following table of values:

t	0.000	0.002	0.004	0.006	0.008	0.010	0.012	0.014	0.016	0.018	0.020
x1
x2

vii. Plot the graphs of x₁ and x₂ on the same axes using any suitable computer package. Extend your table to include x₁ + x₂ and plot this graph on the same axes as the previous two. State the amplitude and frequency of the new wave.

viii. Using your answers from parts v and vii, what conclusions can be drawn about x₁ + x₂ and the two methods that were used to obtain this information?

Task 3.2 -

Scenario: A pipeline is to be fitted under a road and can be represented on 3D Cartesian axes as below, with the x-axis pointing East, the y-axis North, and the z-axis vertical. The pipeline is to consist of a straight section AB directly under the road, and another straight section BC connected to the first. All lengths are in meters.

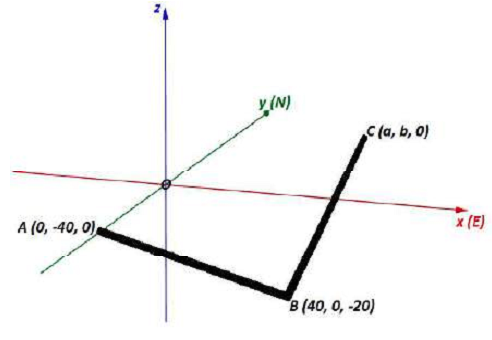
i. Calculate the distance AB.

The section BC is to be drilled in the direction of the vector 3i+4j+k.

ii. Find the angle between the sections AB and BC direction.

The section of pipe reaches ground level at the point C(a, b, 0).

iii. Write down a vector equation of the line BC. Hence find a and b.

Task 4 -

Task 4.1 -

Scenario: The distance x meters moved by a car in a time t seconds is give by x = 4t³ - t² - + 5t +1.

i. Determine the velocity and acceleration when

a) t = 0s

b) t = 2s

Scenario: Cooling curve

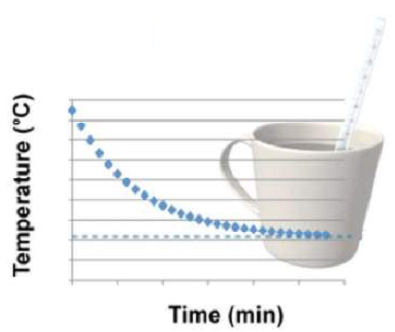
Newtons laws of cooling is given by θ = θ_o e^-kt, where temperature at zero time is θo^oC and at time t seconds is θ^oC.

ii. Determine the rate of change of temperature after 30s, given that θ_o = 20^oC and k = -0.03.

iii. Using a general curve to describe the similarity and difference of maximum and minimum points in a curve.

iv. Find the maximum and minimum value of the curve y = x³ - 12x + 8 by

a) Examining the gradient on either side of the turning points, and

b) Determining the sign of the second derivative

v. Determine the height and radius of a cylinder of volume 300cm³ which has the least surface area.

Task 4.2 -

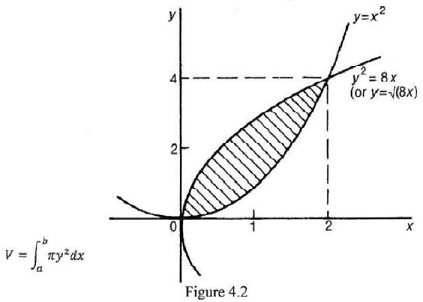
Scenario: In a construction project, a slope excavation is shown by change of slope shape. Use calculus to find the area enclosed by curves represented the prior and final slope shape as shown in Figure 4.2

The two slopes shapes were represented by two curves y = x² and y² = 8x.

i. Use calculus to the area shown by the shaded lines in Figure 4.2.

ii. In this area is rotated 360^o about the x-axis, determine the volume of the soil of revolution produced. The volume of revolution V, obtained by rotating area A through one revolution about the x-axis is given by the following expression:

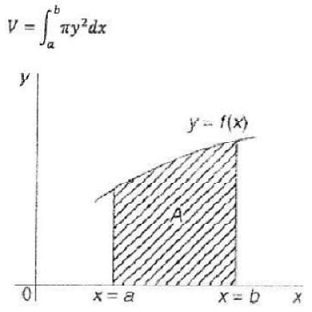
iii. Consider the rate of change equation is dx/dt = kx., where t and x are variable and k is a constant with k ≠ 0.

The number k is called the continuous growth rate if it is positive, or the continuous decay rate if it is negative.

Derive the exponential growth and decay formula by using integration methods.

Attachment:- Assignment File.rar