Reference no: EM13701

Question 1

(a) For the reciprocal lattice, we know that

Exp(jG.R) =1

where G.R = 2Πt, t= an integer;  R= la+mb+nc = real-space/direct translational vector; l, m and n= integers;

G = hp+kq+lr = reciprocal lattice vector normal to the plane in the direct lattice having Miller indices (hkl); and

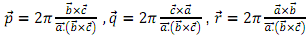
(i) Calculate the reciprocal lattice of the body-centred cubic (bcc) structure.

(ii) Show that the reciprocal of the face-centred cubic (fcc) structure is itself a bcc structure.

(b) Draw (101) and (111) planes in a cubic unit cell. Determine the Miller indices of the directions which are common to both the planes.

(c) A plane makes intercepts of 1, 2 and 0.5 Å on the crystallographic axes of an orthorhombic crystal with a:b:c = 3:2:1. Determine the miller indices of the plane

Question 2

(a) Given that 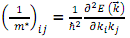and a one-dimensional crystal of lattice constant a, which obeys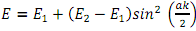

calculate the effective mass of electrons for this energy dispersion relationship.

(b) The following is the E-k dispersion diagram for GaAs:

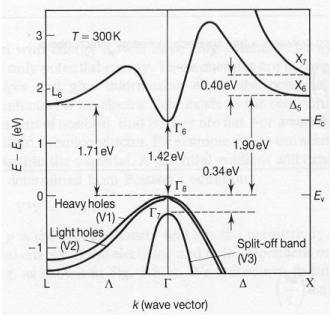
Show that the motion of electrons near the conduction band minimum is isotropic.

(c) For the diagram in part (b) above, explain why two of the allowed energy valence bands (V1 and V2) are referred to as "heavy hole" and "light hole" bands, respectively.

(d) With the aid of simple diagrams show how the presence of a deep acceptor state can reduce the conductivity of n-type semiconductor.

Question 3

Consider a one-dimensional semiconductor with the following expressions for the energy as function of k in the conduction (Ec(k)) and valence (Ev(k)) band:

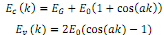
where a is the lattice constant, and E_G and E₀ are positive constants.

In the first Brillouin zone we know that -Π/a ≤ k ≤ Π/a .

(a) What is the minimum energy in the conduction band, and where can it be found in the Brillouin zone?

(b) What is the minimum energy in the valence band, and where can it be found in the Brillouin zone?

(c) What is the band gap energy of this material?

(d) Sketch the band structure in the first Brillouin zone, explicitly showing the energies in each band at the zone centre and the zone edge.

(e) Is this material a direct or indirect band semiconductor?

(f) What is the conduction band effective mass at the conduction band minimum?

(g) What is the conduction band effective mass at k=0?

Suppose an electron in the conduction band can be described by a wavepacket made up from k-states in the small range of k round about k= Π/a.

Question 4

Assume that the E(k) relationship for electrons in the conduction band of a hypothetical tetravalent n-type semiconductor can be approximated by

E = ak² + constant

The cyclotron resonance for electrons in a field of B=0.1T occurs at an angular rotation frequency of ωc =1.8 x 10¹¹ rad.S^-1.

Given 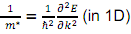 and cyclotron resonance frequency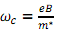 

(a) Find the value of a

(b) Assume that the semiconductor is doped with pentavalent donors. Estimate the number of donors per cubic metre, given that the Hall coefficient at room temperature R_H= -6.25x10^-6  m³C^-1 and the relative dielectric constant ε_r = 15.

Optical excitation of intrinsic Ge creates an average density of 10¹² conduction electrons per cubic centimetres in the material at liquid nitrogen temperature. At this temperature, the electron and hole mobilities are equal, μ = 5000 cm² /Vs.

The Ge relative dielectric constant is 20. We also know that conductivity , and the Einstein diffusion coefficient relationship D/μ = k_gt/q where all terms have their usual meaning.

(c) If 100 volts is applied across a 1 cm cube of Ge crystal under these conditions, approximately how much current is observed?

(d) What is the approximate value of the diffusion coefficient for the electrons and holes?

Question 5

(a) The electron and hole mobilities in a Si sample are 0.135 and 0.048 m² /V-s respectively. Determine the conductivity of intrinsic Si at 300 K if the intrinsic carrier concentration is 1.5×10¹⁶ atoms/m³. The sample is then doped with 10²³ phosphorous atoms/m³.

Determine the equilibrium hole concentration, conductivity and position of the Fermi level relative to the intrinsic level.

(b) The resistivity of an intrinsic semiconductor is 4.5 Ωm at 20°C and 2 Ωm at 32°C. Calculate the energy band gap.

Question 6

(a) The energy near the valence band edge of a crystal is given by

E = -Ak²

where A= 10 Jm . An electron with wave vector k= 10 kx m is removed from an orbital in the completely filled valence band. Determine the effective mass, velocity, momentum and energy of the hole.

(b) In intrinsic GaAs, the electron and hole mobilities are 0.85 and 0.04 m²/V-s, respectively and the corresponding effective masses are 0.068 m₀ and 0.5 m₀, where m₀ is the rest mass of an electron. Given the energy band gap at 300 K as 1.43 eV, determine the intrinsic carrier concentration and conductivity.

Question 7

(a) An electron is presumed to be represented by a wavepacket centred initially around k=0 in the otherwise empty conduction band of a hypothetical one-dimensional crystal. The conduction band of the crystal has the dispersion relation between energy E and wavevector k E = A[1- cos(ka)], where A is a constant and a is the lattice constant. An electric field E is applied along the axis of the crystal (the x-axis) in the positive direction. Assuming that the crystal is perfect and that there is no scattering of the electron, write an expression for the velocity v of the electron as a function of

time. Remember group velocity 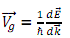, and force

(b) Suppose we have a crystal that has orthorhombic symmetry (three mutually perpendicular axes in the x, y and z directions, but all of different lengths). As a consequence of the crystal symmetry, there is now no requirement that the properties of the crystal should look the same in the three crystal directions. The crystal has one conduction band minimum centred at k=0 (i.e. in the middle of the Brillouin zone), and the electron energy in that minimum obeys the equation

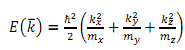
This corresponds to a constant energy surface that is ellipsoidal, but is not an ellipsoid of revolution; the cross-sections in each of the three coordinate directions are ellipses.

What is the density-of-states effective mass mDS in this material?

Question 8

(a) The electron is represented by a wave function y for which E = hω = hν where ω=2πν= corresponding radian frequency of the wave. Show that the group velocity (vg) and effective mass (m*) of the electron in one dimension are given by the following expressions:

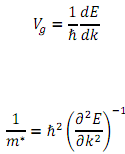
(b) A hypothetical semiconductor has a band structure in one dimension of the form E = Eo[1-cos(ka)],

where Eo= 1.5 eV and a = 5Å. What are the group velocity and effective mass at the following points in this band structure?

(i) k=0;

(ii) k=π/4a;

(iii) k= π/2a;

(iv) k= π/a.

(c) An electron is presumed to be represented by a wavepacket centered initially round k = 0 in the otherwise-empty conduction band of a hypothetical one-dimensional crystal. The conduction band of the crystal has the dispersion relation between energy E and wavevector k

where A is a constant, and a is the lattice constant. An electric field F is applied along the axis of the crystal (the x axis) in the positive direction. Assuming that the crystal is perfect and there is no scattering of the electron, write an expression for the velocity, v, of the electron as a function of time.