Reference no: EM132848150

Mathematics Assignment -

Q1. Find parametric equations for the circle of radius 2 with center (1, 1). Use the equations to find the points of intersection of the circle with the x- and y-axes.

Q2. Find a parametric curve c(t) = (x(t), y(t)) that traces the line y = 2x + 1 from (1, 3) to (3, 7) for 0 ≤ t ≤ 1.

Q3. Find the equation of the tangent line to the curve c(t) = (t³+t, t²-1) at the point c(3), i.e., when t = 3.

Q4. Find the speed (as a function of t) of a particle whose position at time t is c(t) = (sin(t)+t, cos(t)+t). What is the particle's maximum speed?

Q5. Find the length of the curve c(t) = (3e^t - 3, 4e^t + 7) for 0 ≤ t ≤ 1.

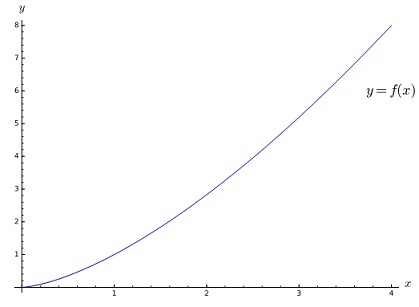
Q6. Below is a plot of the graph of f(x) = x^3/2 over the interval [0, 4]. Parametrize this curve, then use your parametrization to find the length of the curve.

Q7. Suppose given c(t) = (e^-t cos(t), e^-t sin(t)) (a spiral in towards the origin). Show that c(t), for 0 ≤ t ≤ ∞, has finite length, and calculate this finite length. [Hint: Set up, then evaluate, a suitable improper integral.]

Q8. Consider the graph of y = sin(x) from x = 0 to x = π/2 (one half of the first arch of the sine wave). Suppose we want to find the length of this part of the graph.

(a) Parametrize this curve, then use your parametrization to write an integral whose value is the length of the curve.

(b) From part (a), you should have the length of the curve as ₀∫^π/2 v(t) dt, where v(t) is the speed of the curve. However, our techniques from earlier in the semester are not sufficient to evaluate this integral (this is common for arc-length integrals). Instead, approximate the integral, and hence the length of the curve, as follows: Find T₂(t), the second Taylor polynomial of v(t) about t = 0. Then, since v(t) ≈ T₂(t) for t relatively close to t = 0, evaluate

₀∫^π/2 T₂(t) dt

to give an approximation to the length of the curve.

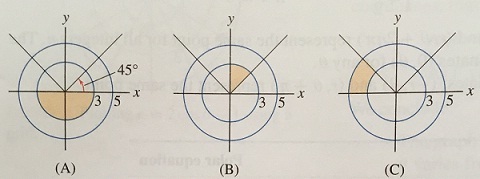
Q9. Describe each shaded region by inequalities in r and θ.

Q10. Convert the polar equation r = 2 sin(θ) into an equation in rectangular coordinates. What curve does this equation describe?

Q11. Match each equation with its description.

(a) r = 2 (b) θ = 2 (c) r = 2 sec(θ) (d) r = 2csc(θ)

(i) Vertical line (ii) Horizontal line (iii) Circle (iv) Line through origin

Q12. Suppose r = f(θ) is the function whose graph is plotted below (in the ordinary, rectangular sense).

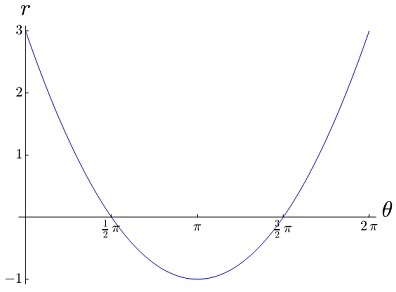
Identify which one of the graphs plotted below is that of the polar curve r = f(θ).

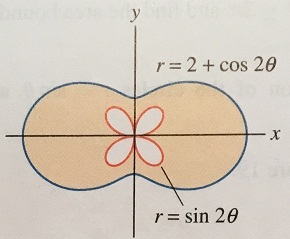
Q13. Find the area between the two curves (the shaded region).

Q14. The polar curve r = 10θe^-θ is plotted for 0 ≤ ∞ ≤ π. Find the area of the region shaded.