Find out the proportion increases

Assignment Help Mathematics

Reference no: EM132315218

Assignment -

Consider a graph G with adjacency matrix A and a random walk on G with transition matrix T, where

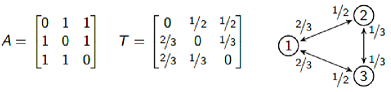
Now our random walker slightly favours vertex 1 over the other two, with neither of these other two being favoured over the other.

So the steady state vector should have the form S =.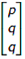

But what should the probabilities p and q be? Can you guess?

To find p and q we could use the method we used when investigating Markov chains earlier in the course.

That is, we could use the computer to solve the system of linear equations represented by the matrix equation (T' - I)S = 0 modified by replacing all entries in the last row of both T - I and 0 by 1.

However, in this case the equations boil down to: -p + 4/3q = 0 and p + 2q = 1.

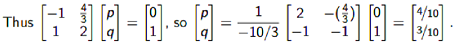
On average, our walker spends 40% of the time at vertex 1 and 30% at each of the other two vertices. Is that what you guessed?

The steady state vector is S =. As you can check, T'S = S.

Please show the solution step-by-step.

For this question, working is not required and will not be marked.

Early in Section D3 of the course we investigated examples of random walks on a 3-vertex digraph under various sets of transition probabilities. This question continues and extends that investigation. The diagram at right shows the transition probabilities for Example 3 in the notes.

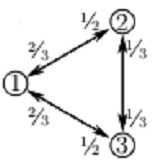
First consider random walks of length 4 starting at 2:

(a) The number of different such walks is.

(b) The number of these walks that end up at 1 is.

Hint: You can either add the probabilities of taking each of the routes you counted for (b), or you can power up the transition matrix using Wolfram Alpha. Doing it both ways is a good check!

Now consider what happens to Example in the notes if vertex 1 is made more 'attractive' by increasing the probability of transition into it from 2/3 to 3/4 (and making the necessary consequential changes to other probabilities - see diagram at left.) As a result of this change we might expect that the probability calculated for part (c) should increase.

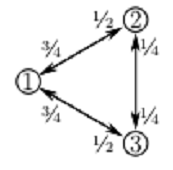
(d) With the new transition probabilities the probability that a length-4 random walk from (2) ends at 1 is. (Give an exact fraction).

(e) Compared to the corresponding probability (c) using the original transition probabilities, this new probability (d) is (circle)

HIGHER / LOWER / THE SAME

As a result of the changed transition probabilities we might also expect that, in the long term, the proportion of time that a random walker spends at vertex 0 will increase, but if so, by how much? Use hand calculations or computer to find out:

(f) The proportion increases from 4/10 to ____.

Instructions: Math Random Walks topic - Handwritten Solution Required.

Attachment:- Assignment File.rar

Reference no: EM132315218

Questions Cloud

Determine and interpret the linear correlation coefficient : Determine and interpret the linear correlation coefficient, and use linear regression to find a best fit line for a scatter plot of the data and make prediction

How do we create an alignment of incentives : Health insurance acts as a buffer between the consumer and cost of health care goods and services. Goods and services cost the consumer less than the charged.

Determine the key components of talent management : Envision an organization (profit, nonprofit, product-or service-driven) with 200 people in which 20 are identified leaders. Formulate a talent management.

Compare and contrast the two costing systems : Job order manufacturing and process manufacturing are two major costing systems used in manufacturing. Compare and contrast the two costing systems.

Find out the proportion increases : Use hand calculations or computer to find out The proportion increases from 4/10 to ____. Compared to the corresponding probability

Discuss about the talent management research priorities : Considering the vast number of diverse groups represented in the workforce, create a brief research agenda that addresses how talent management strategy can.

Determine the key components of talent management : Determine the key components of talent management, including identifying, assessing, and developing talent. Assess how the talent management strategy should.

Discuss program of hr metrics and workforce analytics : Do you believe that a program of HR metrics and workforce analytics might be useful in Regional Hospital? What opportunities do you see regarding where.

What business analytics benefits are highlighted in the case : What Business Analytics benefits are highlighted in the case? What specific examples are used in the case study to support the use of Business Analytics?

User Account

All Pages