Reference no: EM1373138 , Length: 1100 Words
Question 1: What do you mean by a social welfare function? If you suppose that such a function exists, what properties of social optima would be considered by you? Discuss these properties.
Question 2: Assume that there is a pure exchange economy with 2 consumers and 2 goods. The endowments are w1 = (2, 4), w2 = (4, 3). Consumers are or else identical and they have utility function U(x, y) = x1/3y1/3.
a) Make an Edge worth Box for this economy.
b) Give a definition of Pareto Optimal Allocation in this economy. Find out all Pareto optimal allocations and graph them in the Edge worth Box.
c) How would you define a competitive equilibrium for this economy? Solve for the equilibrium and check whether the competitive equilibrium is Pareto Optimal.
Question 3: Two players first simultaneously declare Yes or No. If any of the players declares No, then each player gets 80. If both players declare yes, then they play the given game:

Find out all the subgame-perfect equilibria of the whole game including pure strategies only.
Question 4: What is the theory of Second Best? Prove the theorem by using a diagram.
Question 5: Let the optimal incentive plan be given as:
s (x) = wx+ k where
s(x)= incentive scheme
x = output, w = wage and k = constant 4
A worker can produce x units of output at a cost of C (x) = x2/2 and he can achieve a utility level of u = 0 working elsewhere. What is the optimal wage-labor incentive scheme s(x)1 for this worker?
Section B:
Question 6: Suppose Kareena's utility function is u = (y/1000)1/2. Her initial income when healthy is 36,000. Though, there is a 50% chance that she will face financial loss on being taken ill and the income is likely to decrease by 20,000.
a) Find out the expected value of her income.
b) What expected utility she will have given the possible state of her health?
c) What is the risk premium she will be willing to pay to cover the risk of sickness?
Question 7: Consider the given game given in extensive form:
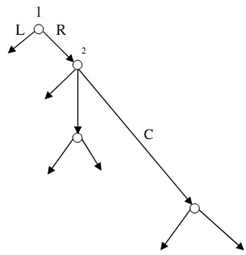
a) Use backwards induction to calculate equilibrium of the game.
b) Write this game in the normal form.
|
Computing expected return on stock
: The risk-free rate is 8%. The beta of stock B is 1.5, and expected return on the market portfolio is 15%. Suppose the capital-asset-pricing model holds.
|
|
Estimation of the stock current price
: A firm at present pays a dividend of $2.00 per share, It is estimated that the firm's dividend will grow at a rate of 20 percent per year for the next 2 years,
|
|
Find the value of company equity
: Edwards Construction currently has debt outstanding with a market value of $80,000 and cost of 12 percent. The firm has an EBIT rate of $9,600 that is expected to continue in perpetuity.
|
|
Determine the risk neutral probability of stock
: Suppose a 6-month put option on a stock with a strike price of $32. The current stock value is $30 and over the next six months it is expected to rise to $36 or fall to $27.
|
|
Find out all pareto optimal allocations and graph
: Give a definition of Pareto Optimal Allocation in this economy. Find out all Pareto optimal allocations and graph them in the Edge worth Box and also describe what is the theory of Second Best? Prove the theorem by using a diagram.
|
|
Determine the company current stock price
: The Zumwalt Corporation is expected to pay a dividend of $2.25 a share at the end of the year, and that dividend is expected to increase at a constant rate of 5.00 percent per year in the future.
|
|
Computing stock beta
: Suppose that the risk free rate is 8 percent and the expected rate of return on the market is 18 percent.
|
|
Determine the expected rate of return on market portfolio
: Determine the Expected Rate of Return on Market Portfolio given that the Expected Rate of Return on Asset 'i' is 10%, Risk-Free Rate is 3 percent, and the Beta for Asset 'i' is 1.5.
|
|
Evaluating the performance of a mutual fund
: Suppose you have just read the yearly report of a mutual fund. It boasted of a 26 percent return and advertised that it had beaten the market return last year by 3% points.
|