Reference no: EM13809920
1. The functions f : {1, 2, 3} → {a, b} and g : {a, b} → {x, y, z} are given by f(1) = b, f(2) = b, f(3) = a, g(a) = y, g(b) = x.
(a) Classify each of f and g as bijective, injective, surjective, or neither.
(b) Find g ? f .
(c) Either find the inverse of g ? f or explain why g ? f is not invertible.
2. I want to develop a database of information about my book collection, which tells me about the authors and genres of the various books I own. At the moment I have books by Isaac Asimov, China Mieville, Peter F Hamilton and Arthur C Clarke, and I denote the set of authors by A = {A, M, H, C}, abbreviating each author by the initial of his surname. I am classifying the books as science fiction, fantasy, horror and non-fiction, so my set of genres is G = {s, f , h, n}, again using initial letters as abbreviations.
At the moment, I have science fiction works by China Mieville and Isaac Asimov, I have fantasy by Peter F Hamilton and China Mieville, horror by Peter F Hamilton and Arthur C Clarke, and non-fiction by Isaac Asimov.
(a) Give the relation R on A × G which represents this information. (You may use appropriate abbreviations.)
(b) Find the combination of projection and inverse projection maps which finds all authors by whom I have horror books.
(c) Find the combination of projection and inverse projection maps which find all writers who have written non-fiction or fantasy books in my collection.
3. (a) Draw the graph with adjacency matrix
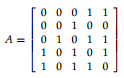
where the columns and rows label vertices 1 to 5 in order.
(b) Use the adjacency matrix connectivity algorithm, starting by marking row 1 and crossing out column 1, to show whether this graph is connected.
(c) Calculate A 2 and hence find the number of paths of length 2 from vertex 1 to vertex 5.
(d) Find a breadth first spanning tree starting at vertex 3.
4. Use Dijkstra's algorithm to find the shortest path from node a to node f in the following graph.
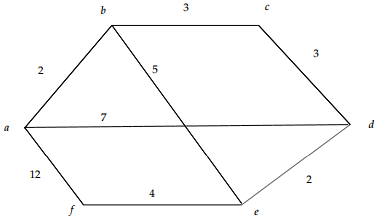
5. Use the heapsort algorithm to put the following list of numbers in decreasing order:
8 2 4 7 1 3 5
You should explain in detail how the original heap is obtained, and then show your sequence of heaps and partial ordered lists.
6. Consider the symbols and frequencies:
o : 12 e : 10 n : 4 t : 6 s : 5 m : 3
(a) Find a Huffman code for this situation, and the average length of an encoded symbol.
(b) Assign the symbols to these codewords in a different order, and comment on the resulting average length.
7. Bob decides to use n = 221 = 13 × 17 and e = 11 as his public key for an RSA cryptosystem.
(a) Show that the decryption exponent is 35.
(b) Find the encrypted form of the message 16.