Reference no: EM131238904
1. Consider the following labelled graph
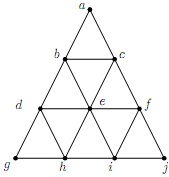
(a) State an upper-bound and a lower-bound on the vertex-chromatic number of the graph, and give reasons for your answers.
(b) Find an optimal colouring of the graph.
(c) To which of the following classes does the graph belong: chordal graphs, trees, bipartite graphs, perfect graphs? Provide reasons for your answers.
(d) Beginning with the matching M = {(e, f )}, extend M into a maximum matching by repeatedly finding augmenting paths. At each step you should increase the number of edges in the matching by one. Explicitly show each step of the process.
Recall: an augmenting path is an alternating path that joins two "exposed" vertices. An edge between two exposed nodes is also regarded as an augmenting path.
(e) State a lower-bound on the edge-chromatic number of the graph, and give a reason for your answer.
2. Suppose teachers x1, x2, x3, x4 have to teach classes y1, y2, y3, y4, y5, y6 according to the following teacher/class allocation table:
|
|
y1
|
y2
|
y3
|
y4
|
y5
|
y6
|
|
x1
|
0
|
0
|
1
|
0
|
1
|
1
|
|
x2
|
1
|
0
|
1
|
0
|
0
|
2
|
|
x3
|
1
|
1
|
1
|
0
|
0
|
1
|
|
x4
|
2
|
0
|
0
|
1
|
1
|
0
|
(a) What is the minimum possible number of periods used in this allocation. How do we know this without doing a decomposition?
(b) Calculate the minimum number of periods using a single 1's decomposition.
(c) Construct a timetable using the minimum number of periods.
3. For n Ç 3, find the number of distinct perfect matchings in the cycle Cn of length n. Justify your answer.
4. Suppose that T is a tree (a connected graph without cycles) with n vertices and that every vertex of T has degree 1 or 3.
(a) Prove rigorously that n is even.
(b) Prove rigorously that T has exactly (n + 2)/2 leaves (vertices of degree 1).
|
Synthesize appropriate current research
: Research Paper paper that investigates a specific natural disaster topic, apply critical thinking to the presentation of the information, and utilize and synthesize appropriate current research for your selected topic.
|
|
Determine an expression for the fundamental axial mode shape
: Determine an expression for the fundamental axial mode shape, φi(x), and use M a t l a b , or another computer program, to plot the fundamental mode. Scale the mode so that.its maximum value is l.CL
|
|
Plywood firm uses three inputs-labor-lumber and saws
: A plywood firm uses three inputs – labor, lumber, and saws. Although it van vary its labor each week, it must order its lumber six months in advance, and it would take a year for the firm to sell its saws or acquire new saws. What time periods compri..
|
|
Provide a succinct and accurate definition
: Suppose I say to you: "My belief that God exists is rational and false." What do I mean when I say that? Provide a succinct and accurate definition of what the textbook calls a "biased" belief. (Provide a definition that fits with the other concep..
|
|
Find an optimal colouring of the graph
: MAST20018 - Discrete Mathematics and Operations Research State an upper-bound and a lower-bound on the vertex-chromatic number of the graph, and give reasons for your answers - Find an optimal colouring of the graph.
|
|
What is concept of family most used in your area of nursing
: What is the concept of family most used in your area of nursing practice? Is it the most helpful concept for considering family in nursing practice? Why?
|
|
What was the approximate value of walminus
: Recall the Application about the size of Walminus−Mart to answer the following? question(s). During? 2008, Walminus−?Mart's sales were approximately? $374 billion, or roughly 2.6 percent of U.S.? GDP, and its cost of sales was? $286 billion. Accordin..
|
|
Why managers hire the wrong person
: Why managers hire the "wrong" person? How to overcome the problem mentioned about?
|
|
How the selected product could be used by your client
: Discussion of how the selected product could be used by your client to support its cybersecurity objectives by reducing risk, increasing resistance to threats/attacks, decreasing vulnerabilities, etc.
|