Reference no: EM131281288

Ecological Footprint (EF)

The Ecological footprint (EF) measures how much of the regenerative capacity of the biosphere is used up by human activities. It is the sum of productive land and water area required to support the population and provide the resources it consumes, absorb its waste and provide infrastructure (Stiglitz et al., 2009, p. 244, https://www.insee.fr/fr/publications-et-services/default.asp?page=dossiers_web/stiglitz/documents- commission.htm). Biocapacity is a measure showing the capacity of biosphere to regenerate and provide for life. More detailed definitions are given on page 5.

Figure 1: Humanity's ecological footprint by component 1961-2012

Figure 2: Ecological footprint and Biocapacity per capita 1961-2012

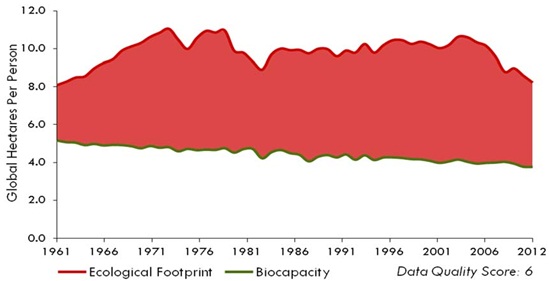
Figure 3: United States of America: Ecological footprint and Biocapacity per capita 1961-2012

1. According to the EF, is the human population living at, beyond or below the Earth's natural biocapacity? For how long has this been the case? Is this sustainable?

2. According to the EF, is the US population living at, beyond or below USA's natural biocapacity? For how long has this been the case? Is this sustainable?

3. If you assume that EF grows at a constant yearly rate, what is the approximate slope of the EF relationship with time for USA? And what is its units? Give the equation of, and sketch this line, with EF on the vertical axis and year on the horizontal axis. (EF for 2012 is 8.2 and for 1961 was approximately 8.1).

4. If you assume that biocapacity grows at a constant yearly rate, what is the approximate slope of the biocapacity relationship with time for USA? And what is its units? Give the equation of, and sketch this line, with biocapacity on the vertical axis and year on the horizontal axis. (biocapacity for 2012 is 3.8 and for 1961 was approximately 5.2).

5. If this trend continues, what will EF and biocapacity be in 2050? (Hint: use your equation from questions 3 and 4.) What will biocapacity minus EF be in 2050? Will there be a deficit or reserve?

6. Use the data presented in Figure 1 to suggest a policy to make land use sustainable.

Part A

Planet Issues - Unlimited Population Growth

One way to think about the growth of some biomass---whether a petri dish full of bacteria or a river full of fish--- as some fixed proportion of the existing population. The unlimited population growth model is a simple model which assumes that, in each period, some fixed proportion b of a population will reproduce, and some fixed proportion d will die.

The model describes the evolution of a population over time, t.

N(t) = N_Oe^(b-d)t, (1)

where N0 is the population at time t=0.

1. If the initial population N0=3000, the annual birth rate b=0.04 (4% exponential birth rate) and annual death rate d=0.03 (3% exponential death rate), what is the population after 1 year? Explain this result.

2. Find an expression for the growth rate of the population in terms of b, d and N(t). Hint: remember that differentiating with respect to time gives a rate of change.

3. If d < b, will the expression you found in the previous part be positive or negative? How would you interpret this fact?

Part B

Planet Issues - Unlimited population growth with harvesting

The model in equation (1) describes a population untouched by humans: there is no harvesting. We can model what happens if we harvest H individuals from the population each period. The unlimited population growth with harvesting model is given by

N(t) = ae^(b-d)t + K-Ke_(b-d)t/(b-d), (2)

where b is the birth rate, d is the death rate, and H is the number of individuals taken from the population in each period.

1. Confirm that the rate of population change is

dN(t)/dt = (b - d)N(t) - H. (3)

Hint: differentiate (2), then add (+H-H), and rearrange so that you can substitute (2) back in.

2. Give the meaning of the expression in (3).

3. Let N0=N(0)=3000, b=0.06 and d=0.02. At what rate can the population be harvested sustainably? Hint: The sustainable harvest, H, will be the value that causes no change in the overall population, i.e. dN(t)/dt = 0.

4. Suppose an ecosystem is being sustainably harvested at exactly its replacement rate, and the population is constant. Now suppose the population experiences a brief disease epidemic, which causes 6% of individuals to perish. What will happen to the population if harvesting continues at the same rate?

5. Suppose a population of fish that follows this model is being harvested sustainably, as before. What will happen in the long run if, one day, a fisherman decides to throw one of the fish back?

6. This type of model is often said to have a "knife-edge" equilibrium. Explain what this means.

7. Governments often levy fishing quotas in areas where populations are at risk. Does this model shed any light on the effectiveness (or otherwise) of these policies? (Hint: what if someone cheats?)

Part C

Planet Issues - The Verhulst model of ecological growth

We now consider a slightly more sophisticated version of the above model. Leaving harvesting to one side for a minute, we will consider what happens when there is a limit to growth. The previous model assumed that populations could continue to grow indefinitely. Empirical research suggests that there tends to be a limit to the size of population that an environment can support; we call this limit the carrying capacity, K.

A model linking these ideas was first proposed by a French mathematician Pierre Verhulst in 1838. The Verhulst model can be written as:

N(t) = 1+ N_O(e^rt)/N_O(e^rt-1)  (4)

where N0 is the initial population level (Bacaër, 2011). For simplicity, we'll write the net reproduction rate simply as r, rather than in terms of births and deaths.

1. What is the growth rate if the initial population is zero?

2. When the population is initially at its carrying capacity, i.e. N0 =K, what is the population at time t? How does the population level change when the growth rate r increases?

3. Differentiate (4) to show that the rate of population growth at time t is

dN(t)/dt = rN(t) (1 - N(t)/ K) (5)

Remember to use the quotient rule to differentiate (4). You will find it easier if you carefully look for the terms that you expect to see in the final expression, and factor those out.

4. Does the population grow faster when it is above the environment's carrying capacity (N>K), or below it (N<K)?

5. A pond has a carrying capacity of 500,000 fish. Its population this year is 450,000 individuals. If the reproduction ratio is r = 5%, and the population follows the Verhulst population model, how many fish can be harvested per year, leaving a constant population?

6. Suppose that, due to unlicensed fishing, the population falls by half, to 225,000. How many fish can be harvested per year, in order to maintain a stable population? Explain the difference between the previous question and this question.