Reference no: EM132232563

Lamoureux Assignment -

Exercise 1 - It's Valentine's Day. Plot a cardioid curve. (A curve in the 2D plane that looks like a heart.)

(In 3D, the heart surface looks like the following image. See Wolfram's MathWorld to see the polynomial involved in the "heart surface." Matlab also has code to plot this!)

Exercise 2 - More on Kepler's law.

Suppose you have a mass m sliding on a frictionless table, attached to a pole at the center of table via an elastic spring. The force due to the spring is proportional to the distance from the mass to the center of the table

F = k · ()

It turns out the mass will move around the table in an ellipse, say of some mean radius $R$ and period of oscillation T.

Use dimensional analysis to show the period T depends on the mass m and the spring constant k. Show explicitly what the power law is, for this relationship.

How is this different from Kepler's third law?

Can you conclude that the Earth is not connected to the Sun via a big spring?

Exercise 3 - Can you solve the above system numerically? You might like to use the SciPy function "odeint" to solve this.

Plot your results, so that you can see the mass really does move in an ellipse.

Note: the 2D system of equations would look something like:

m d²x/dt² = -kx, (1)

m d²y/dt² = -ky, (2)

So for odeint, you will need to use a 4 dimentional vector, that involves functions (x, x', y, y').

You might notice that the above system is easy enough to solve explicitly (i.e. solved for x, y, as explicit functions of time). But do try it numerically.

Exercise 4 - A more complicated Buckingham Pi example.

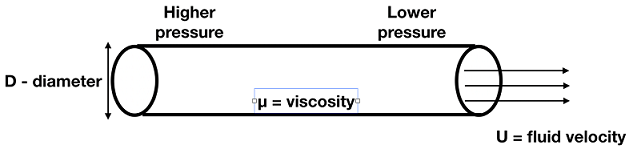
Picture a long pipe, a viscous fluid flowing in it. The pressure is high on the left, low on the right, so there is a pressure gradient that causes the fluid to flow.

There are 5 physical parameters for this:

• D, the diameter of the pipe
• ρ, the density of the fluid
• μ, the dynamic viscosity of the fluid
• U, the average velocity of the fluid
• P' = dP/dx, the gradient of the pressure (assumed constant in the pipe).

Part 1: Show there are 3 physical units, so by Buckingham Pi, there are 5-3 = 2 independent, unitless quantities Π₁, Π₂. Find them. (Hint: one might be the Reynolds number. Always a good choice.)

Part 2: Since there are two Π's, we can expect to "solve the problem" in the form

Π₂ = F(Π₁)

for some unspecified function F.

Use this approach to find the constant pressure gradient P' as a product of powers of D, ρ, U and F(Π₁).

Exercise 5 - Find an expansion for the roots of the cubic

εx³ + x - 1 = 0

for small values of ε. Find three (non-zero) terms in each expansion.

Exercise 6 - Set-up: The logistic equation (from calculus)

du/dt = ku(1-u)

is a simple model for population growth when there are limited resources. For instance, think of rabbits in a field of grass that they can eat. When there are just a few rabbits (u close to zero), the equation becomes

du/dt ≈ ku,

and we get exponential growth. When u is close to 1, the rabbits run out of grass, and the equation becomes

du/dt ≈ σku,

which gives slow growth or slow decay towards 1, depending on whether σ = 1-u is positive or negative.

Exercise: Now, suppose the problem has a periodic perturbation (say due to seasons of grass growing):

du/dt = ku(1 + εcos(t) - u).

Find a periodic solution u = 1 + εu₁(t) + ··· which is correct to O(ε). That is, the error is of O(ε²).

Exercise 7 - (This is related to a trick we used in the traffic flow problem. Good to review.)

The temperature T = T(x, y, z) of a body in three dimensions, that has cooled to steady state, will satisfy the second order differential equation ∇·(k(T)∇T) = 0, where k(T) is the thermal conductivity of the material, which often depends on temperature.

This is NOT Laplace's equation. Show that making a change of variables u = ∫^Tk(s)ds

we get Laplace's equation

∇²u = 0

Hint: You might like to start off in 1 dimension, T = T(x) to understand the steps. Then try T = T(x, y, z).

Note also that the definition of u as an anti-derivative is kind of written in a shorthand notation. Make sure you make good sense of this, to obtain a function u = u(x, y, z). Be careful here, and then it all works out nicely.

Attachment:- Assignment Files.rar