Reference no: EM13983069

1: Consider the function H given   by

           2x + 2    for   x < 1

H(x) =

           2x - 4    for  x ≥ 1

a) Graph the function.

b) Find lim_x→1 H(x) both numerically and graphically.

c) Find lim_x→-3 H(x) both numerically and graphically.

2: Calculate the following limits based on the graph of f .

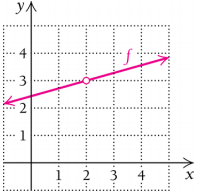
a) lim_x→2- f(x)

b) lim_x→2+ f(x)

c) lim_x→2 f(x)

3: Find  lim_x→0 √ (x² - 3x + 2).

4: Find the following limits and note the Limit Property you use at each step:

a) lim_x→1 2x³ + 3x² - 6

b) lim_x→4 2x² + 5x - 1/3x - 2

c) lim_x→2√(1 + 3x²)

5: Find lim_x→-3 (x² - 9/x + 3).

6: Is the function f given by f (x) = x² - 5, continuous at x = 3?  Why or why not?

7: Is the function g given by

             1/2x + 3                for  x <  2

g(x) =

             x - 1                      for  x ≥ -2

continuous at x = -2?  Why or why  not?

8: Is the function g given by

           (x² - 9/x - 3)      for   x ≠ 3

h(x) =

                 7             for   x = 3

continuous at x = 3?  Why or why not?

9: Let    

             (x² - 25/x-5)       for   x ≠ 5

 p(x) =

                    c                          for x = 5

Determine c such that p is continuous at    x = 5.

10: State the average rate of change for each situation in a short sentence. Be sure to include units.

a) It rained 4 inches over a period of 8 hours.

b) Your car travels 250 miles on 20 gallons of gas.

c) At 2 P.M., the temperature was 82 degrees. At 5 P.M., the temperature was 76 degrees.

11: For f (x) = x², find f'(x). Then find f'(-3) and  f'(4).

12: For f (x) = x³, find f'(x). Then find f'(-1) and f'(1.5).

13: For f (x) = 3/x:

a) Find f'(x).

b) Find f'(2).

c) Find an equation of the tangent line to the curve at x = 2.

14: Find each of the following derivatives:

a) d/dx(5x³ - 7)

b) d/dx(24x - √x +(5/x))

c) d/dx(3x⁵  + 2³√x +(1/3x²) + √5)

15: Find the points on the graph of f (x) = -x³ + 6x² at which the tangent line is horizontal.

16: Find:

a) d/dx[(x⁴ - 2x³ - 7) (3x² - 5x)]

b) d/dx [(2x⁵ + x - 1) (3x - 2)]

c) d/dx [(√x+1)(⁵√x - x)]

 17: Differentiate and simplify your result:

a) f (x) = x² - 3x/ x - 1

b) g(x) = 1 - 3x/x² + 2

18: Paulsen's Greenhouse finds that the cost, in dollars, of growing x hundred geraniums is given by  C(x)  =  200 + 100 •  ⁴√x.   If  the  revenue  from  the  sale  of  x  hundred  geraniums  is  given  by R(x) = 120 + 90 • √x, find each of the following.

a) The average cost, the average revenue, and the average profit when x hundred geraniums are grown and sold.

b) The rate at which average profit is changing when 300 geraniums are being grown.

19: Differentiate f (x) = (1 + x³)^1/2.

20: Differentiate f (x) = (3x - 5)⁴(7 - x)¹⁰.

21: Differentiate f (x) = 2x² - 1/(3x⁴ + 2)².

22: GameBoss Video's profit, in dollars, is given by y = f (u) = 0.1u² - 500, where u is the   number of units sold. Its sales are given by u = g(x) = 125x + 40, where x is the number of days. Find the rate at which profit is changing on the 5th day.

23: For y = 1/x, find d²y/dx².

24: For y = (x² + 10x)²⁰, find and simplify y' and y''.

25: Find y'':

a) y = -6x⁴ + 3x²

b)  y = 2/x³

c)  y = (3x² + 1)²

26: For s(t) = 10t²  find v(t) and a(t), where s is the distance from the starting point, in miles, and t is in hours.  Then, find the distance, velocity, and acceleration when t = 4  hr.