Find a relation between the mean velocity and pressure drop

Reference no: EM13799349

1. You design a tent ceiling with conical pores. How should you orient the cones in the ceiling to keep the rain droplets trapped in the pores. Explain your choice using Laplace equation and taking into account the gravity effect and the difference in the advancing and receding contact angles.

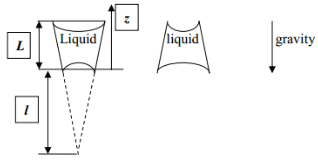
2. A liquid bridge of length /, density p, and surface tension a, is trapped in a cylindrical capillary of radius r

a) Assuming that the liquid bridge is sitting a halfway down to the lower end of the capillary and the advancing contact angle is θ_a and receding contact angle is θ_r, find a critical condition when the liquid bridge becomes unstable and will fall down the capillary.

b) Assuming that the lower end of the liquid bridge is sitting at the capillary edge (i.e. the contact angle is not defined), analyze the shape of the lower meniscus as a function of the length of the liquid bridge. Setting the condition of meniscus detachment as θ_a = 90°, find the critical length of the liquid bridge for σ = 0.1 N/m, ρ = 1000kg/m₃, R = 0.1 mm.

3. A die in the extrusion box is made of a slit and a tube connected in a chain. The channels have the same opening H and length L. H is the gap thickness for a slit and H is the diameter for a tube. The width of the slit is W. Find a relation between the mean velocity and pressure drop applied to the ends of this device.

4. A container with water is connected with the atmosphere by a cylindrical pipe of diameter d= 1 cm and 10 cm length.

a) Find the time T at which the liquid column decreases by two times? Analyze the dependence T=T(h) using Matlab.

b) Find the time T at which the liquid column decreases by two times if container is connected with the atmosphere by a slit-like pipe of diameter d= 1 cm, and 10 cm length, and width W = 1cm.

Reference no: EM13799349

Questions Cloud

What is kings tone in the given latter : Read Letter to Birmingham by Martin Luther king and it asks "What is Kings tone in the first paragraph and how might you make an argument for its being ironic?

Individual assignment popular literature paper : Individual Assignment Popular Literature Paper

Natural vegetation regions of sub-saharan africa : With respect to global connections, association with _______ offers the brightest immediate future for many African countries.

Determine the main benefits of using graphs in the report : determine the main benefits of using graphs in the report presentation. Next, explain the matter in which a creatively constructed graph might help you to better manage and present your data.

Find a relation between the mean velocity and pressure drop : A die in the extrusion box is made of a slit and a tube connected in a chain. The channels have the same opening H and length L. H is the gap thickness for a slit and H is the diameter for a tube. The width of the slit is W. Find a relation betwee..

Bringing change to public leadership : Bringing Change to Public Leadership

Write about interracial marriage and students in classroom : Write a paper about Interracial Marriage and Students in Today's Classroom.

Overproduce goods with external costs : Use graph to illustrate your answer. Explain why market tend to overproduce goods with external costs. Given the graph below, show the CS and PS on the graph. Define consumer surplus and calculate its size.

Motion of a person diving : This question models the motion of a person diving from a 10-metre board into a swimming pool. The whole motion may be split into two phases, above and below the water.

User Account

All Pages