Reference no: EM131523220

Q1. (a) Determine the truth value of the statement, give reasons for your answer.

(∀x ∈ R) (∃y ∈ R) ((y ≥ 0 ∧ y = x) v (x < 0 ∧ y = -x)).  

(b) Show that the statement ∃x∀yP(x, y) = ∀y∃xP(x, y) is universally valid, i.e. is true for any interpretation of the predicate P(x, y) in a non-empty domain U common for all quantifiers.

(c) Prove by contraposition that if a + b < 2n, then either a < n or b < n where the universe is the set of real numbers R. Write down the corresponding formal statement in Predicate Logic.

Q2. (a) Prove that if A and B are sets with A - B ⊆ B, then A ⊆ B. Do not use Venn diagrams.

(b) Let A be a set with precisely 4 elements, that is, |A| = A. Compute (just give final answer):

(1) |A x A| =

(2) |P(A)| =

(3) |P(P(A))1| =

(4) |A ∪ A| =

(5) |A ∩ A| =

(6) |A - A| =

(c) For sets A, B, C, D, let f : A → B and g : C → D be functions.

Let h : A x C → B x D be defined by

h((x, y)) = (f (x), g(y)) for all (x, y) ∈ A x C.

(i) Assume that f and g are both injective. Prove that then h is also injective.

(ii) Assume that f and g are both surjective. Prove that then h is also surjective.

Q3. (a) Show that f (x) = 5x⁴ + 3x² + 2x + 1 is Θ(x⁴) by directly finding the least possible witnesses.

(b) Give as good a big-O estimate as possible (in terms of the standard reference functions) for the function

f(n) = n log(n³ + 1) + (n + 1) log(n!) + _k=1Σⁿk, where n is a positive integer.

Q4. (a) Determine whether each binary relation R on the set Q of rational numbers is reflexive, symmetric, anti-symmetric, or transitive where xRy if and only if

(i) x ≠ y.

(ii) xy ≥ 1

(b) Find the equivalence classes [1] and [1/2] of 1 and 1/2 respectively for the equivalence relation R on R : (a, b) ∈ R. iff a - b ∈ Z.

Q5. Prove by induction

(a) _k=1Σⁿk⋅2^k = (n-1)2ⁿ⁺¹ + 2, n ≥ 1.

(b) 1 + 1/√2 + 1/√3 + ⋅ ⋅ ⋅ + 1/√n > √n, n ≥ 2.

Q6. (a) For the Fibonacci sequence defined recursively by f₀ = 0, f₁ = 1, and f_n+1 = f_n + f_n-1 for all n ≥ 1 prove that

f_n+1 f_n-1 - f_n² = (-1)ⁿ for all integers n ≥ 1.

(b) Show that the set S ⊆ Z defined by 1 ∈ S and s + t ∈ S whenever s ∈ S and t ∈ S is the set of positive integers Z⁺.

Q7. (a) Find a recurrence relation and give initial conditions for the number of bit strings of length n that contain at least 3 consecutive zeroes.

(b) How many bit strings of length 8 contain at least 3 consequtive zeroes?

Q8. (a) Solve the recurrence relation

a_n = -5a_n-1 - 6a_n-2 + 42 ⋅ 4ⁿ, n ≥ 2

with initial conditions a₀ = 16, a₁ = 65.

(b) (i) Which complete bipartite graphs K_m,n are trees?

Let T be a full 8-ary tree with 201 vertices.

(ii) How many internal vertices does T have?

(iii) How many leaves does T have?

Q9. (a) Determine whether the digraphs G and H below are isomorphic.

(b) For which values of n are the graphs K_n and C_n bipartite?

(c) Show that in a finite simple undirected graph with at least two vertices there must be two vertices of the same degree.

Q10. (a) Can someone cross all the bridges shown in this map exactly once and return to the starting point?

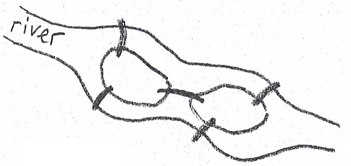
 (b) For which values of m and n does the complete bipartite graph K_m,n have an

(i) Euler circuit?

(ii) Euler path?

(iii) Hamilton circuit?

(iv) Hamilton path?

Please provide detailed steps for the proofs.