Reference no: EM131548585

Question 1

Let g(x)=x-3 and h(x)=x^2+6. Find (h o g) (1).

Question 2

Find a quadratic equation function that includes the set of values

(0,6), (2,14), (4,-2).

Question 3

determine if Ax = b has a unique solution for every b in R⁴

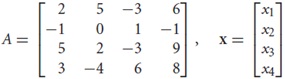
Question 4

Maximize: 4x₁ + 5x₂

subject to the constraints:

x₁ + 2x₂ ≤ 10

6x₁ + 6x₂ ≤ 36

         x₂ ≤ 4

         x ≥ 0, y ≥ 0

Question 5

Let V be the set of all positive real numbers. V is a vector space with the following operations:

x + y = xy (addition)

cx = x^c (scalar mutliplication) c ∈ R

Verify each vector space axiom (There are ten listed below)

Definition of a Vector Space

Let V be a set on which two operations (vector addition and scalar multiplication) are defined. if the listed axioms are satisfied for every u, v, and w in V and every scalar (real number) c and d, then V is called a vector space.

Addition:

1. u + v is in V.    Closure under addition

2. u+v=v+u          Commutative property

3. u + (v + w) = (u + v) + w  Associative property

4. V has a zero vector 0 such that for every u in V, u + 0 = u.  Additive identity

5. For every u in V, there is a vector in V denoted by -u such that u + (-u) = 0.  Additive inverse

Scalar Multiplication:

6. cu is in V.             Closure under scalar multiplication

7. c(u + v) = cu + cv               Distributive property

8. (c + d)u = cu + du             Distributive property

9. c(du) = (cd)u      Associative property

10. 1(u) = u                Scalar identity

Question 6

Give the equation of the oblique asymptote, if any, of: f(x) = (-6x³ - 7x² - 6x + 9) / (2x + 1)

a. y = 0
b. y = -3x - 2
c. no oblique asymptote
d. -3x² - 2x - 2

Question 7

The formula r = ³√3V/4Π gives the radius of a sphere in centimeters for a Volume V given in cubic centimeters. Find r to the nearest tenth of a centimeter if the Volume is 2,744 cubic cm.
 
Question 8

The coast-down time "y" for a car as it drops 10 mph from an initial speed "x" depends on several factors such as air, drag, tire pressure, and if transmission is in neutral. Use a quadratic regression feature to find the quadratic function "g" that best guts the data. Round to four decimal places.

Use model to predict coast down time at initial speed of 70 mph.

Question 9

Find a polynomial with integer coefficients that has degree 3, and zeros 0 and i.

Question 10

T(x₁, x₂, x₃) = (-2x₂ -2x₃, -2x₁ + 8x₂ + 4x₃, -x₁ -2x₃, 4x₂ + 4x₃)

Determine whether the linear transformation T is one-to-one.