Reference no: EM131394646

Problems to solve:

1. Let P denote the vector space of all polynomials with real coefficients. This is an infinite dimensional vector space. Consider the inner product on P defined by

(f(x), g(x)) = ₀∫¹ f(x)g(x)dx.

The vector space P₂(R) is a subspace of P.

(a) Compute proj_{P_2(R)} (x³) and perp_{P_2(R)}(x³).

(b) Give an example of a non-zero polynomial f(x) ∈ P such that proj_{P_2(R)}(f(x)) = 0.

(c) Suppose f(x) ∈ P,

₀∫¹f(x) dx = 0,     ₀∫¹xf(x)dx = 0,    ₀∫¹x²f(x)dx = 1.

Given an example of a polynomial f(x) satisfying these conditions. Is it possible to determine proj_{P_2(R)}(f(x)) from the information given? If so, what is it? If not, explain why.

2. Let A be an m x n matrix. Let L: Row(A) →Col(A) be the linear map defined by L(x^→) = Ax^→. Prove that L is an isomorphism.

3. (a) Let A be an k x n matrix, and leb B be an l x n matrix. Prove that Null(B) = Row(A) if and only if Null(A) = Row(B).

(b) Consider the matrix

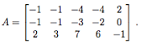
Find a matrix B such that Null(B) = Row(A).

(c) Consider the matrix

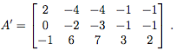
Find a basis for Row(A) ∩ Row(A').

(Note: the rows of A' are just the rows A in reverse. You may find this helpful.)

4. Let W be the subspace of M_2x2(R) spanned by

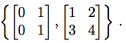
(a) Find an orthonormal basis for W^⊥.

(b) Let S =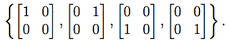

Compute s[proj_W]s and s[perp_W]s.

6. Let V be a finite dimensional inner product space, and let W be a subspaces of V. Prove the following statements.

(a) For all x^→,y^→∈V, (x^→,y^→) = (proj_W(x^→), proj_W(y^→)) + (perp_W(x^→), perp_W(y^→)).

(b) Suppose v^→∈V. There exists a vector x^→∈W such that (v^→, x^→) = 1 if and only if v^→∉ W^⊥.

(c) If dim W = k and dim V = n, then exists a basis β for V such that

Β[proj_W]_β = [e^→₁                  e^→₂     . . .     e^→_k   0^→    0^→    . . .     0^→],

(The first k columns of the matrix are standard basis vectors e^→₁, . . . , e^→_k ∈ Rⁿ, and  the last n - k columns of the matrix are 0^→ ∈ Rⁿ.)