Reference no: EM132399036

FIN 3618 Financial Econometrics, Norwegian Business School

1. In the following exercise, you will work with an updated version of the data used in G¨urkaynak, Sack, and Wright (2007).1 Open this homepage, read the abstract, and click on "Data - Excel file" to download the data. To decrease the file size, open "feds200628.xls" (the file you just downloaded) in Excel, convert it into an xlsx file, and save it as "feds200628.xlsx".2 The file contains (among others), thirty time series of continuously compounded yields of zero coupon bonds for maturities varying between one year (SVENY01) and thirty years (SVENY30) on a daily basis from June 14, 1961 to the beginning of October 2019.3,4 Since there are no data available for March 21, 2008, delete all the observations corresponding to this day from your sample. (40 points)

(a) Take a closer look at the time series and choose the sample in such a way that you have the maximal number of observations for each time series and entries for each point in time in all columns of interest (i.e., SVENY01 to SVENY30), i.e., that there are no more missing entries (NaN) in your data.

Plot the following three time series over your chosen sample period: SVENY01, SVENY10, and SVENY30. Then provide three additional plots highlighting the dependence with respect to the time to maturity (i.e., SVENY01, SVENY02,. . . , SVENY29, SVENY30), one for each of the following dates:

March 3, 1989,
January 2, 2007, and
September 1, 2017.

Ignore the different levels in the three plots and focus on the shape of the yield curve only. Which would you refer to as the normal yield curve, i.e., the one we observe in "normal times"? Provide economic arguments for the shape of the normal yield curve.

(b) Calculate all possible correlations between the thirty time series over. Report the value of the smallest correlation and the names of the two time series between which you find this correlation.

(c) Calculate the principal components of the correlation matrix. Specify that the eigenvalues are saved in the vector eigenValues and the corresponding eigenvectors in the matrix eigenVectors. How much of the total variation in the series are explained by the first, second, and third principal component separately and in sum? Do you think it is necessary to include more principal components than these three?

(d) The matrix eigenVectors contains the eigenvectors corresponding to all thirty eigenvalues. Plot the eigenvector corresponding to the each of the first three principal components as a function of the time to maturity. Copy this graph into your solution paper. Can you
provide an interpretation for each of the three principal components shown in the plot?

(e) Finally, you want to make sure that your principal component analysis worked and it really transformed the correlated explanatory variables into uncorrelated principal components. To standardize each of the thirty time series, subtract from each observation the mean
of the time series and divide the result by the standard deviation of the time series. Next, multiply the matrix containing all the standardized time series with the matrix of eigenvectors to compute the time series of the thirty principal components. Calculate all possible correlations between the thirty principal components - but do not report it in your solution paper! Instead describe the pattern the correlation matrix shows. Did your principal component analysis work?

2. Follow the steps outlined in Appendix A and download the daily stock return time series of Colgate-Palmolive from WRDS. Next, open Kenneth French's homepage and download the "Fama/French 5 Factors (2x3) [Daily]". The file contains the daily time series of the five
factors Fama and French (2015, 2016) propose as an extension of their conventional threefactor model in which they suggest two new factors: operating profitability and investment.

Thus they consider the following five factors:

R^e_M,t (Market Minus Risk-free): the simple average return on the market minus the simple average risk-free rate.

SMB_t (Small Minus Big): the simple average return on the portfolio containing small stocks minus the simple average return on the portfolio containing big stocks.

HML_t (High Minus Low): the simple average return on the portfolio containing value stocks minus the simple average return on the portfolio containing growth stocks.

RMW_t (Robust Minus Weak): the simple average return on the portfolio containing stocks with robust operating profitability minus the simple average return on the portfolio containing stocks with weak operating profitability.

CMA_t (Conservative Minus Aggressive): the simple average return on the portfolio containing stocks with conservative investment strategies minus the simple average return on the portfolio containing stocks with aggressive investment strategies.

Moreover, the last column contains the daily time series of the simple return on the U.S.

- Treasury bill with one month to maturity which we will use as a proxy for the risk-free rate in this exercise. Note that the Fama-French factors and the risk-free rate are expressed in percentage points whereas the returns on Colgate-Palmolive are in decimal points.

(a) Use the five Fama-French factors at time t as the independent variables and the excess return of Colgate-Palmolive at time t as the dependent variable, i.e., run the following regression:

R^e_CP,t = β₁ + β₂ R^e_M,t + β₃ SMBt + β₄ HML_t + β₅ RMW_t + β₆ CMA_t + u_CP,t.

Summarize the parameter estimates, their t-statistics, and the adjusted R² in a table in your solution paper. Based on a significance level of 5%, which of the variables are statistically significantly different from zero? Is there a variable you would consider deleting from the regression? Explain your answer. For each variable which is statistically significant, provide an assessment of its economic significance by looking at the impact of a one-standard deviation change in the corresponding independent variable.

(b) For each of the following hypotheses, write down the restricted regression, and provide an economic interpretation. Perform each test using a significance level of 5% and report its results in your solution paper.

i. H0 : β₂ = 0 and β₃ = 0 and β₄ = 0 and β₅ = 0 and β₆ = 0 vs.
H1 : β₂ ≠ 0 or β₃ ≠ 0 or β₄ ≠ 0 or β₅ ≠ 0 or β₆ ≠ 0

For this test, illustrate in detail the steps underlying this test and explain your results from an economic point of view.

ii. H₀ : β₃ = 0 and β₄ = 0 and β₅ = 0 and β₆ = 0 vs.
H₁ : β₃ ≠ 0 or β₄ ≠ 0 or β₅ ≠ 0 or β₆ ≠ 0

iii. H₀ : β₅ = 0 and β₆ = 0 vs.
H₁ : β₅ ≠ 0 or β₆ ≠ 0

(c) You are wondering whether the stock return of Colgate-Palmolive is different for a specific day of the week. Hence, you define the following dummy variables, one for each day of the week:

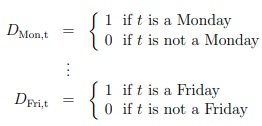
For instance, the Monday dummy variable at day t will be equal to one (D_Mon,t = 1) if and only if t is a Monday. If this is not the case, the dummy variable will be equal to zero (D_Mon,t = 0).

Use the five Fama-French factors at time t as well as the five dummy variables at time t as independent variables and the excess return of Colgate-Palmolive at time t as the dependent variable, i.e., run the following regression without a constant:

R^e_CP,t = β₂ R^e_M,t + β₃ SMB_t + β₄ HML_t + β₅ RMW_t + β₆ CMA_t + β₇ D_Mon,t + β₈ D_Tue,t + β₉ D_Wed,t + β₁₀ D_Thu,t + β₁₁ D_Fri,t + u_CP,t,

so that the dummy variables altogether capture the missing constant. Summarize the parameter estimates, their t-statistics, and the adjusted R² in a table in your solution paper.

Based on these results, can you provide an economic interpretation for the coefficients of the dummy variables that are statistically significantly different from zero?

Attachment:- feds200628.rar