Reference no: EM133063986

FEEG6007 Principles of Photovoltaics, Fuel Cells and Batteries - University of Southampton

Problem sheet 1

Part A

Question 1. What are intrinsic, n-type and p-type semiconductors ?

Question 2. Define the efficiency of a solar cell. Under what conditions is it usually measured ?

Question 3. Write down the current-voltage characteristic of an ideal solar cell. How does it differ from the current-voltage characteristic of a diode ?

Question 4. What are the principal electrical parameters that describe the operation of a solar cell? How do they depend on temperature and irradiance ?

Question 5. Using data given in the lecture notes, would you expect the open-circuit voltage of a crystalline silicon cell to be smaller or larger than for an amorphous silicon cell ?

Question 6. What are the principal current losses in a solar cell ?

Question 7. What are the main steps in the manufacture of a crystalline silicon solar cell ?

Question 8. What principal materials are used in the manufacture of thin film solar cells ?

Question 9. What are the main categories of photovoltaic systems ? What typical components do they usually contain ?

Question 10. What are the roles of the following components of photovoltaic systems ?

Inverter                          Maximum power point tracker
Islanding protection          Charge regulator
Low voltage disconnect     String (blocking) diode
By-pass diode                  Sun tracker

Question 11. What are the principal features of the following applications of solar cells:

Solar powered marine signals                    PV powered irrigation system
Solar power for a satellite                        Building integrated PV system in Germany
A concentrator PV systems                      Solar cell for a calculator
Large solar power station                         Solar array for an isolated holiday home

Part B: True or false ?

1. Cells made from low-bandgap semiconductors usually produce large current.

2. Solar cell can be pictured as a current generator connected in series with a diode

3. The voltage output of a solar cell is directly proportional to the irradiance.

4. The reflectivity of bare silicon is high but decreases to acceptable levels after encapsulating the cells beneath glass.

5. The blocking diode in a stand-alone photovoltaic system is connected in parallel with a string of modules.

6. The photocurrent produced by a photovoltaic generator depends exponentially on the cell temperature.

Part C.

Question 1. The photon spectral flux density in the standard AM1.5 solar spectrum can be approximated by the following function:

φ(E) = 0 (E < a)
φ(E) = k1 (E - a) (b > E ≥a )
φ(E) = k2 (c - E) (c > E ≥ b)
φ(E) = 0 (E ≥ c)

where a = 0.4 eV, b = 0.85 eV, c = 3 eV, k₁ = 7. 55x1017 cm^-2 s^-1 eV^-2 and k₂ = 1.58x10¹⁷ cm^-2 s^-1 eV^-2.

(a) Plot the photon flux density and the corresponding solar spectrum

(b) Plot the graph of the maximum electrical current that can be produced by a 10x10 cm solar cell made from a semiconductor with band gap Eg.

(c) Plot the efficiency of this solar cell as a function of the bandgap Eg assuming that the voltage produced by the cell is equal to (Eg - 0.4), where Eg is in electronvolts and the fill factor is equal to 0.8.

(d) What is the optimum band gap of the solar cell material ?

(e) What is the cell efficiency for this band gap ?

Question 2. Under standard measurement conditions, a solar cell of area 100³ cm has the short-circuit current 3.5A and open-circuit voltage 0.6V. The temperature coefficient of the open-circuit voltage is equal to - 2.3mV/deg C; the short-circuit current can be assumed temperature independent. The fill factor is equal to 0.7 and can be assumed constant. Calculate the cell efficiency in the following situations:

(a) Under standard conditions

(b) Under the irradiance of 0.8 kW/m, with the cell temperature equal to 60°C.

(c) As part of a 50 ×concentrating system, maintaining the cell at 25 C.

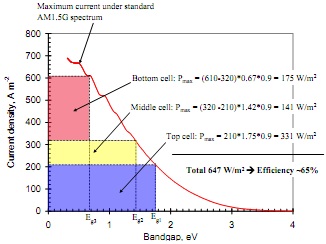
Question 3. Using the graph of maximum current that can be produced by a single junction solar cell and a fill factor of 0.9, estimate the efficiency of GaInP / GaAs / Ge triple-junction ce ll with bandgaps of 1.75, 1.42 and 0.67 eV under maximum concentration of sunlight.

Question 4(a) The load factor of a power generator is defined as the ratio between the delivered energy and the energy that would be produced if the generator operated at the rated power for the full period in question. What is the load factor of a photovoltaic generator in terms of the Peak Solar Hours (PSH) ?

(b) A photovoltaic system is to be installed at an isolated farm with daily solar radiation of 5kWh/m². The generator is to power lighting (350W, used for 4 hours a day) and a water pump (rating 500W, used for 3 hours a day). What size of photovoltaic array (in Wp) and battery (in Wh) would you recommend assuming 6 days of autonomy?

Problem sheet 2

SECTION A

Question 1. Write illustrated notes on TWO of the following:

(a) Draw the graph of a typical cell voltage vs. current density dependence (polarization curve) for a fuel cell and explain the three main characteristic regions. Use equations that define the cell voltage and labeled diagrams to illustrate your answer. What are the major losses of energy?

(b) Explain the concept of cyclic voltammetry and the criteria for a reversible system. Show an example that includes a detailed labelled current vs. potential curve. Explain how the concentration of the electroactive species on the surface of the electrode change as the potential moves away from the equilibrium value.

(c) Explain the principle of redox flow cells. Are they suitable to store large amounts of electrical power? Why? What is the driving force? Illustrate your answer with some examples.

(d) What is the purpose of an ion exchange membrane? Give examples where these membranes are used. Explain which is the main transport mode of ions inside the ionic membranes and why. Mathematical expressions and diagrams should be used.

(e) Explain the difference between galvanic (self-driven) and electrolytic (driven) cells. Give examples of each system and explain the direction of the reaction in terms of Gibbs free energy.

Question 2. Answer ALL parts of this question.

(a) Write the overall cell reaction and the value of the standard cell potential of a galvanic cell that consist of the following half-cell reactions. Clearly indicate what the oxidizing and reducing agents are:

Al³⁺ + 3e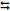^- Al(s)   Ε⁰_Al3+/Al = -1.66 V vs. SHE (1)

Cu²⁺ + 2e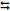^- Cu(s) E⁰_Cu2+/Cu = +0.34 V vs. SHE (2)

(b) Write the notation of the cell indicating the phase boundary and the salt bridge.

(c) Calculate the Gibbs Free Energy change ΔG and the ln K for this reaction where K is the equilibrium constant.

(d) In the following reaction:

Zn(s) + 2H⁺(aq) 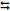Zn²⁺(aq) + H₂(g) The half-cell reactions are:
Zn2+ + 2e- Δ Zn(s) Ε0 = -0.76 V vs. SHE (1) 2H+ + 2e- Δ H2(g) E0 = +0.0 V vs. SHE (2)

i) Write the Nernst equation for the whole reaction and suggest how decreasing the concentration of Zn²⁺ would affect the cell potential, Ecell.

ii) Using the Nernst equation, what is the effect on the cell potential when metallic Zn increases?

iii) What is the standard cell potential of the cell, E0_cell?

iv) What is the real cell voltage of the cell at 25°C when the concentration of [Zn²⁺] is 0.5 M? The partial pressure of hydrogen, pH₂ is 10 atm and the pH is 6.

Faraday constant, F = 96 485 C mol-1, Gas rate constant, R = 8.314 J mol^-1 K-1 273.15°C = 0 K; 25°C 298.15 K
F/RT = 38.92 V^-1
RT/F = 0.02569 V
2.303 RT/F = 0.05916 V

Question 3. Answer ALL parts of this question.
A pilot-scale borohydride - air fuel cell consumes 100 g of fuel per hour.
(a) State the most likely anode-, cathode- and cell reactions and potentials.
(b) If the open-circuit potential of a single cell during operation is 1 V, calculate the theoretical maximum energy in kJ mol-1 and kW h kg^-1 available from the cell.

(c) Calculate the maximum energy available in kJ from the stack in 15 hours.

(d) Calculate the cell current, stating all assumptions.

(e) What is the importance of the cell design for a successful operation of a borohydride fuel cell? State the strategies to achieve high energy from a stack.

SECTION B

Question 4. Answer ALL parts of this question.

(a) A beam of light at a wavelength of 500 nm, with a spectral width of 8 nm and spectral irradiance of 1000 W m^-2 μm^-1, illuminates an area of 10 cm2. Determine the photon flux density in the beam and the power, voltage and current that this beam could generate if converted to electricity.

(b) The standard solar spectrum can be approximated by the following spectral irradiance function (in units of W m^-2 μm^-1) as a function of the wavelength λ (in µm):

e_λ(λ) = 0     (λ < 0.4 µm)

e_λ(λ) = 325/λ³     (0.4 ≤ λ < 3.1 µm)

e_λ(λ) = 0 (3.1 µm ≤ λ)

(i) What is the total photon flux density (in photons per square metre per second) in the spectrum?

(ii) What maximum short-circuit current can be generated by 10 cm x 10 cm crystalline silicon solar cell?

(iii) What is the maximum efficiency of this crystalline silicon solar cell?

(iv) What is the maximum efficiency of a tandem solar cell made from semiconductors with bandgaps of 1 and 2 eV?

Hint: You may wish to convert first the spectral irradiance as a function of λ into a function of photon energy.

Electron charge q = 1.602 x 10-19 C Bandgap of crystalline silicon = 1.12 eV Where appropriate, use a fill factor ff = 0.75

Question 5: Answer ALL parts of this question.

(a) Concisely discuss technologies that are available for the manufacture of solar cells which are available commercially as well as those under development in research laboratories. Your discussion should include brief notes about the expected efficiencies, costs, status of development and / or market penetration and possible applications.

(b) A 15% efficient crystalline silicon solar cell is manufactured from a 350 μm thick silicon wafer. Assuming 200 μm kerf loss in wafering, what is the silicon usage (in grams per Wp) in the cell manufacture?

(c) A solar cell has an open-circuit voltage of 0.7 V, short circuit current 3.5 A and efficiency 20% under standard test conditions. It operates at a temperature of 25 C under concentrated sunlight with a concentration ratio of 10. What short-circuit current, open circuit voltage and efficiency would you expect in this case?

Boltzmann constant kB = 8.61 x1^0-5 eV K^-1 Temperature conversion 0 C = 273.15 K Silicon density = 2.33 g cm^-3

Question 6. Answer ALL parts of this question.

(a) With the help of simple circuit diagrams where appropriate, describe concisely the roles of the following components in a photovoltaic system:
• charge regulator
• maximum power point tracker
• islanding protection
• by-pass diode
• blocking diode
• load (low voltage) disconnect

(b) A photovoltaic module, consisting of 36 crystalline silicon solar cells, has an open - circuit voltage of 21 V and a short - circuit current of 3 A. The series resistance of one cell has been determined to be 40 mΩ. If the fill factor ff_o of a similar ideal solar cell (without series resistance) is 0.892, what is the power of this module at the maximum power point?

(c) What is the dark saturation current of one cell in the module in Part (b) under standard test conditions?

(d) How many of the modules in Part (b) and how large battery (in Wh) would you need to power a daily load of 300 Wh in a location with daily solar radiation of 4.5 kWh m^-2, for a system that operates without a maximum power-point tracker, having 6 days of autonomy?