Reference no: EM132432235

Programme title - BTEC Higher National Diploma in Computing

Unit Number and Title - Unit 18 Discrete Mathematics

Assignment Title - Discrete mathematics in Computing

Unit Learning Outcomes:

1. Examine set theory and functions applicable to software engineering.

2. Analyse mathematical structures of objects using graph theory.

3. Investigate solutions to problem situations using the application of Boolean algebra.

4. Explore applicable concepts within abstract algebra.

Activity 1 -

Part 1 -

1. Let A and B be two non-empty finite sets. If cardinalities of the sets A, B, and A ∩ B are 72, 28 and 13 respectively, find the cardinality of the set A ∪ B.

2. If n(A - B) = 45, n(A ∪ B) = 110 and n(A ∩ B) = 15, then find n(B).

3. If n(A) = 33, n(B) = 36 and n(C) = 28, find n(A ∪ B ∩ C).

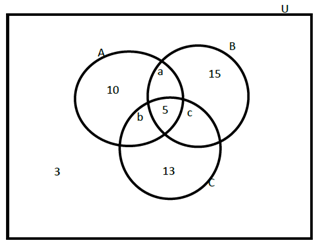
Part 2 -

1. Write the multi-sets of prime factors of given numbers.

I. 160

II. 120

III. 250

2. Write the multiplicities of each element of multisets in part 2(1-I,ii,iii) separately.

3. Find the cardinalities of each multiset in part 2-1.

Part 3 -

1. Determine whether the following functions are invertible or not. If it is invertible, then find the rule of the inverse (f^-1(x))

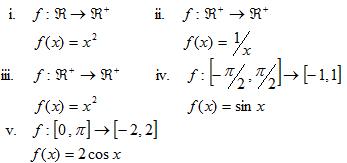
2. Function f(x) = 5/9 (x-32) converts Fahrenheit temperatures into Celsius. What is the function for opposite conversion?

Part 4 -

1. Formulate corresponding proof principles to prove the following properties about defined sets.

i.

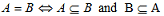
ii. De Morgan's Law by mathematical induction.

iii. Distributive Laws for three non-empty finite sets A, B, and C.

Activity 2 -

Part 1 -

1. Discuss using two examples on binary trees both quantitatively and qualitatively.

Part 2 -

1. State the Dijkstra's algorithm for a directed weighted graph with all non-negative edge weights.

2. Find the shortest path spanning tree for the weighted directed graph with vertices A, B, C, D, and E given using Dijkstra's algorithm.

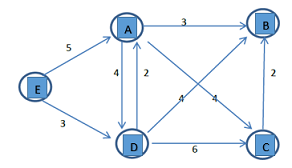
Part 3 -

1. Check whether the following graphs have an Eulerian and/or Hamiltonian circuit.

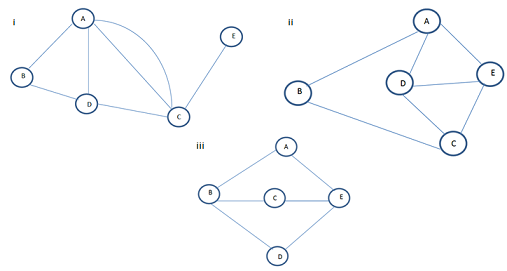
Part 4 -

1. Construct a proof for the five color theorem for every planar graph.

2. Discuss how efficiently Graph Theory can be used in a route planning project for a vacation trip from Colombo to Trincomalee by considering most of the practical situations (such as millage of the vehicle, etc.) as much as you can. Essentially consider the two fold,

- Routes with shortest distance(Quick route travelling by own vehicle)

- Route with the lowest cost

3. Determine the minimum number of separate racks needed to store the chemicals given in the table (1st column) by considering their incompatibility using graph coloring technique. Clearly state you steps and graphs used.

Chemical	Incompatible with
Ammonia (anhydrous)	Mercury, chlorine, calcium hypochlorite, iodine, bromine, hydrofluoric acid (anhydrous)
Chlorine	Ammonia, acetylene, butadiene, butane, methane, propane, hydrogen, sodium carbide, benzene, finely divided metals, turpentine
Iodine	Acetylene, ammonia (aqueous or anhydrous), hydrogen
Silver	Acetylene, oxalic acid, tartaric acid, ammonium compounds, pulmonic acid
Iodine	Acetylene, ammonia (aqueous or anhydrous), hydrogen
Mercury	Acetylene, pulmonic acid, ammonia
Fluorine	All other chemicals

Activity 3 -

Part 1 -

1. Discuss two real world binary problems in two different fields using applications of Boolean algebra.

Part 2 -

1. Develop truth tables and its corresponding Boolean equation for the following scenarios.

i. ''If the driver is present AND the driver has NOT buckled up AND the ignition switch is on, then the warning light should turn ON.''

ii. If it rains and you don't open your umbrella then you will get wet.

2. Produce truth tables for given Boolean expressions.

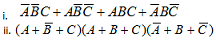
Part 3 -

2. Find the simplest form of given Boolean expressions using algebraic methods.

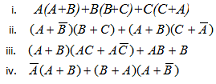
Part 4 -

1. Consider the K-Maps given. For each K- Map.

i. Write the appropriate standard form (SOP/POS) of Boolean expression.

ii. Draw the circuit using AND, NOT and OR gates.

iii. Draw the circuit only by using

i. NAND gates if the standard form obtained in part (i) is SOP.

ii. NOR gates if the standard form obtained in pat (i) is POS.

(a)

AB/C	0	1
00	0	0
01	0	1
11	0	1
10	1	0

(b)

AB/CD	00	01	11	10
00	1	0	0	1
01	0	1	0	1
11	1	1	1	0
10	1	1	1	1

(c)

AB/C	0	1
00	1	0
01	1	1
11	1	0
10	0	1

Activity 4 -

Part 1 -

1. Describe the characteristics of different binary operations that are performed on the same set.

2. Justify whether the given operations on relevant sets are binary operations or not.

i. Multiplication and Division on se of Natural numbers

ii. Subtraction and Addition on Set of Natural numbers

iii. Exponential operation: (x, y) → x^y on Set of Natural numbers and set of Integers.

Part 2 -

1. Build up the operation tables for group G with orders 1, 2, 3 and 4 using the elements a, b, c, and e as the identity element in an appropriate way.

2. i. State the Lagrange's theorem of group theory.

ii. For a subgroup H of a group G, prove the Lagrange's theorem.

iii. Discuss whether a group H with order 6 can be a subgroup of a group with order 13 or not. Clearly state the reasons.

Part 3 -

1. Check whether the set S = R - {-1} is a group under the binary operation '*'defined as a * b = a + b + ab for any two elements a, b ∈ S.

2. i. State the relation between the order of a group and the number of binary operations that can be defined on that set.

ii. How many binary operations can be defined on a set with 4 elements?

3. Discuss the group theory concept behind the Rubik's cube.

Part 4 -

1. Prepare a presentation for ten minutes that explains an application of group theory in computer sciences.