Reference no: EM13935220

The Fibonacci Sequence and Generalizations

The purpose of this set of exercises is to introduce you to the much-studied Fibonacci sequence, which arises in number theory, applied mathematics, and biology. In the process you will see how useful eigenvalues and eigenvectors can be in understanding the dynamics of difference equations.

The Fibonacci sequence is the sequence of numbers

0,1,1,2,3,5,8,13,....

You can probably see the pattern: Each number is the sum of the two numbers immediately pre-ceding it; if yk is the kth number in the sequence (with y0 = 0), then how can y100 be found without just computing the sequence term by term? The answer to this question involves matrix multiplication and eigenvalues. The Fibonacci sequence is governed by the equation

yk+2 = yk+1 + yk,

or

yk+2 ^-yk+1 ^-yk = 0.

If you have studied Section 4.8, you will recognize the last equation as a second-order linear difference equation. For reasons which will shortly become apparent, a trivial equation is added to get the following system of equations:

yk+1 = yk+1
yk+2 = yk+1 + yk

To see how linear algebra applies to this problem, let

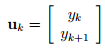
The above system of equations may then be written as

u_k+1 = Au_k

where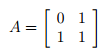 

To ?nd yk, just look at the bottom entry in u_k. The vector uk could be written in terms of u₀ by noting that

u_k = Au_k-1 = AAu_k-2 =...= A^ku₀

The ?rst goal is to ?nd an easy way to compute A^k. This is where eigenvalues and eigenvectors enter the picture.

Questions:

1. Using your technology, compute A5 and use it to ?nd u5 and y5.

2. Show that the eigenvalues of A are

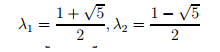
by solving the characteristic equation of A.

3. Show that

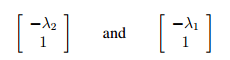
are eigenvectors of A corresponding to λ1 and λ2 respectively. You may ?nd it helpful to note λ1 + λ2 = 1 and λ1λ2 = -1.

4. Explain why A is diagonalizable.

5. Find (by hand) a matrix P and a diagonal matrix D for which A = PDP-1.

6. Use your technology to calculate D10, and use it to ?nd A10, u10, and y10. Con?rm your result for y10 by writing out the Fibonacci sequence by hand.

7. A formula for yk may be derived using the following two questions. Use the above expres-sions for P, D, and Ak to show that a general form for A^k is

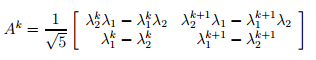
8. Use the result of Question 7 to ?nd uk and yk. Again make note of the fact that λ1λ2 = -1. If you've worked it out all right, you should have found that

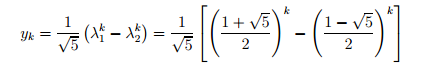
Calculate y10 using this formula, and compare your result to that of Question 6.

9. Notice that the second of the two terms in parentheses is less than 1 in absolute value, so as higher and higher powers are taken, it will approach zero. The following equation results:?_ _ ?1 ? 1 + 5 ? 5 2

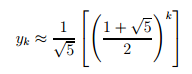
Use this approximation to approximate yk+1/yk.

The approximation for y_k+1/y_k which you found in the last question is called the golden ratio, or golden mean. The ancient Greek mathematicians thought that this ratio was the perfect proportion for the rectangle. That it appears in such a "remote" area as the limiting ratio for the Fibonacci sequence (which occurs in nature in sunflowers, nautilus shells, and in the branching behavior of plants) makes one wonder about the connection between nature, beauty, and number.

The above work on the Fibonacci sequence can be generalized to discuss any difference equation of the form

yk+2 = ayk+1 + byk,

where a and b can be any real numbers.  A sequence derived from this equation is often called  a Lucas sequence. 

Questions:

10. Consider the Lucas sequence generated by the difference equation

y_k+2  = 3y_k+1 - 2y_k,

with y0 = 0 and y1 = 1. Write out by hand the first seven terms of this sequence and see if you can find the pattern. Then repeat the above analysis on this sequence to find a formula for yk .

11. Consider the Lucas sequence generated by the difference equation

yk+2  = 2yk+1 - yk,

with y₀ = 0 and y₁ = 1. Find the pattern by writing out as many terms in the sequence as you need. Will an analysis like that for the Fibonacci sequence work in this case? Why or why not?