Reference no: EM132401393 , Length: 1 pages

Question: Cubic splines.

Suppose you are in charge of the design of a roller coaster ride. This simple ride will not make any left or right turns; that is, the track lies in a vertical plane. The accompanying figure shows the ride as viewed from the side. The points (at , bi) are given to you, and your job is to connect the dots in a reasonably smooth way.

Let a_i+1 > a_i, for i = 0, . . . , n-1.

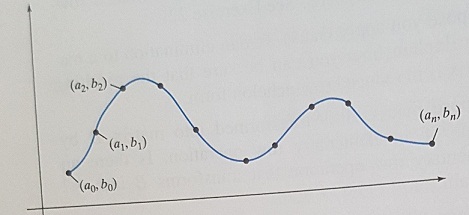
One method often employed in such design problems is the technique of cubic splines. We choose fi(t), a polynomial of degree < 3, to define the shape of the ride between (a_i-1, b_i-1) and (a_i, b_i), for i = 1, . . . , n.

Obviously, it is required that f_i(a_i) = b_i and f_i(a_i -1) = b_i-i, for i = 1, . . . , n. To guarantee a smooth ride at the points (abbi), we want the first and second derivatives of fi and f_{i +1} to agree at these points:

fi'(a_i) = f'_i+1 (a_i) and

fi"(a_i) = f"_i+1 (a_i), for i = 1, . . . , n - 1.

Explain the practical significance of these conditions.

Explain why, for the convenience of the riders, it is also required that

f1'(a₀) = f'n(a_n) = 0.

Show that satisfying all these conditions amounts to solving a system of linear equations. How many variables are in this system? How many equations? (Note: It can be shown that this system has a unique solution.)