Reference no: EM13541536

Problem 1:

Suppose, we have a network in which data transfer requests (or flows) arrive for scheduling at a central server. Suppose that all the requests share a bottleneck link whose capacity is 70+X Mbps (Mega bits per second), where X = (Your roll number) modulus 20. The bottleneck link in the path of a flow is the link with the smallest available capacity. Suppose that the inter-arrival times of the requests (or flows) are exponentially distributed but the data size and the transfer duration of the flows is constant (same for all flows). The minimum required data transfer rate of a flow is obtained by dividing its data size with its transfer duration. The data transfer rate of a flow can increase (if bandwidth is available) during its transfer at any stage. The link is always fully utilized if there is at least one flow using that link. A request is rejected if its required transfer rate is not available at its arrival time.

a) Identify and explain the events that can change the state of the system

b) Suppose the arrival times of the first 10 requests are 1, 3, 5, 6, 7, 8, 11, 12, 14, 15 seconds (of simulation time). The data size of each flow is 180+Y Mega bits, where Y = (Your roll number) modulus 30, and the transfer duration of each flow is 5 seconds. Fill the following table.

Problem 2:

Jobs arrive at a server according to a Poisson input process at a rate of four per day, and the service time has an exponential distribution with a mean of 1/5 per day. Enough-in-process storage space is provided at the server to accommodate five jobs in addition to the one being processed. Determine the percent of time that this storage space will be adequate to accommodate newly arrived jobs.

Problem 3:

Traffic to a message switching center for one of the outgoing communication lines arrive exponentially at an average rate of 220 messages per minute. The line has a transmission rate of 880+B characters per second, where B = (Your roll number) modulus 40. The message length distribution (including control characters) is exponential with an average length of 170 characters. Hence, the service times of messages are also exponentially distributed. Calculate the following principal statistical measures of system performance, assuming that a very large-sized (infinity) message buffer is provided:

(a) Average number of messages in the system
(b) Average number of messages in the queue waiting to be transmitted.
(c) Average time a message spends in the system.
(d) Average time a message waits for transmission
(e) Probability that 10 or more messages are waiting to be transmitted.

Problem 4: Extend (by 10 more rows) and fill the table. Consider two repairmen for the machine-repairman problem.

Operational time of each machine = 6+C units of time, where C = (Your roll number) modulus 3

Repair time for each machine = 6 units of time

CL1, CL2, CL3 are associated with machines 1, 2, 3 respectively

CLR1 and CLR2 tell repairman 1's and 2's completion time respectively

At t=0, all three machines are operational, CL1=2, CL2=5, CL3=5+D units of time, where D = (Your roll number) modulus 3.

Problem 5: The CDF of exponential distribution is F(x) = 1-e-ax. Write a programming code to generate 100 random variates according to exponential distribution and store them in an array.

Problem 6:

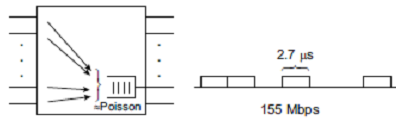
The output buffer of an ATM multiplexer can be modeled using a queue. Constant service time means that an ATM cell has a fixed size (53 octets; each octet is of 8 bits) and its transmission time to the link is constant. If the link speed is 155 Mbps, then the transmission time is S = 53* 8/155 μs = 2.7μs. What is the mean number of cells in the buffer (including the cell being transmitted?) and the mean waiting time of the cell in the buffer when the arrival rate on the link is 80+A Mbps, where A = (Your roll number) modulus 20?