Reference no: EM131890123

Questions:

1. Using a suitable empirical example, explain how a logit model can be estimated using maximum likelihood estimation.

2. Explain the difference between marginal effects at the averages and average marginal effects in the context of a probit model.

3. Using an empirical example, explain the use of a receiver operating characteristic analysis.

4. Using a numerical illustration if necessary, discuss the steps of the Hosmer-Lemeshow goodness-of-fit test in the context of the estimation of binary choice models.

5. A researcher estimates a logit regression model of the probability of exporting based on data from 300 firms (100 exporters and 200 non-exporters), and reports the following result:

ft_i = F(-1.24 + 0.560size_i + 0.262PROF_i)

In the above function, Π^{^} denotes the estimated probability of exporting, F (.) is the logistic probability function, SIZE is log of firm size and PROF is log of profits. Give the precise expression for the average marginal effect of firm size on the probability of exporting.

6. Consider a multinomial logit model with four categories and two regressors. Write down the relevant conditional probabilities, and derive the expressions for calculating the marginal effects of the regressors.

7. What is the Independence of irrelevant alternatives (IIA) assumption in the context of multinomial models? Using an empirical illustration outline a testing procedure to test the IIA assumption.

8. Consider an ordered logit model with three categories and two regressors- one continuous and the other binary. Assuming that there are N cross-sectional observations, (i): Write the log likelihood function of the ordered logit estimator; (ii) Give the expression for the variance-covariance matrix of the resulting maximum likelihood estimator; and (ii) Give precise expressions for all relevant average marginal effects.

9. An economist asked 1580 workers to categorise themselves as unsatisfied (satisfied=0), neither unsatisfied nor satisfied (satisfied=1), moderately satisfied (satisfied=2) and very satisfied (satisfied=3). The individuals were also asked to report the number of hours they work per week (hours) and how much they earn (wages). Based on this information, the following ordered probit model of the determinant of individuals' work satisfaction is estimated:

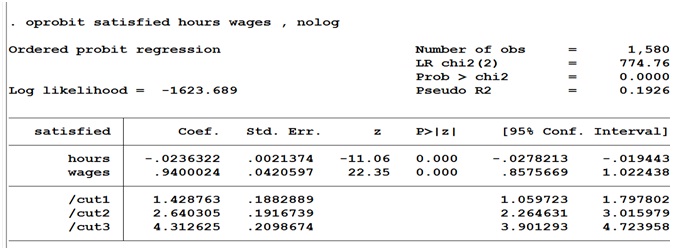
(i) Write down the log likelihood function used to estimate the model parameters, explaining all the notations you have used.

(ii) Based on the estimated model parameters, give the precise expressions for calculating the average marginal effect of wages on the probability of being moderately satisfied.

10. Using an empirical example, give a brief explanation of the estimation of alternative-specific conditional logit models, and the interpretation of the estimated regression parameters.

11. This is a computer exercise, and you need to access the mortgage default data (mortgage.dta) from the module's page. The idea is to estimate mortgage default models using different combinations of the following regressors: rate (interest rate); lvr (loan amount to value of property in %; insur (1 if borrower has mortgage insurance; 0 else); amount (loan amount in £100,000); credit (applicant's credit score); vrm (= 1 if variable rate mortgage, 0 if fixed).

(i) Estimate the 6 models specified in the table below, and fill in the empty columns.

(ii) Based on the completed table (or indeed on further estimations you might like to carry out), choose your preferred model. Based on the chosen model, generate some marginal effects and write a short report on your findings.

Program fragment using model 3 as an example: