Reference no: EM134443
Question 1
One subway station in Toronto has six turnstiles, each of which may be controlled by the station manager to be used for either entrance or exit control - but never for both. The manager must decide at different times of the day just how several turnstiles to use for entering passengers and how many to be set up to allow exiting passengers.
Consider that passengers enter the station at a rate of about 84 per minute between the hours of 7 and 9 A.M. Passengers exiting trains at the stop reach the exit turnstile area at a rate of about 48 per minute during the same morning rush hours. Each turnstile will allow an average of 30 passengers per minute to enter or exit. Service and Arrival times have been thought to follow Poisson and exponential distributions, respectively. Consider riders form a common queue at both entry and exit turnstile areas and proceed to the first empty turnstile.
The station manager does not want the average passenger at his station to have to wait in the turnstile line for more than six seconds, nor does he want more than eight people in any queue at any average time.
a) How many turnstiles should be opened in each direction every morning?
b) Show the assumptions underlying the solution of this problem using queuing theory.
Question 2
Consider the subsequent network, where the numbers represent actual distance between the corresponding nodes.
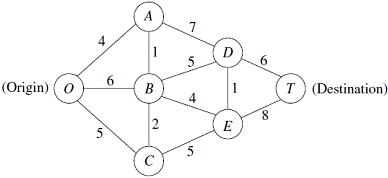
a) Use the algorithm described to evaluate the shortest path from O to T.
b) Formulate this shortest path problem as an integer programming problem and solve it in EXCEL.
Question 3
A computer engineer lives in town A and needs to visit each of the towns B, C, D, and E to service various installations. He must visit each town once and return to town A. The distances in miles between the towns are shown in the table.
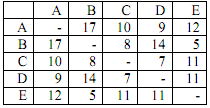
a) Use the nearest neighbor algorithm to find a tour, starting at town A.
b) Use the nearest insertion algorithm to find a tour, starting at town A.
c) Use Clarke and Wright savings algorithm to find a tour, starting at town A.