Reference no: EM131159

1. Evaluate the sequence generated by each of the following generating functions.

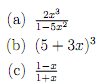
2. For each of the subsequent generating functions, nd the coecient of x¹⁵ .

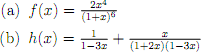
3. Find a closed form generating function (i.e. not a series) for each of the following given sequences.

(a) 0; 0; 0; 2; 0; 2; 0; 2; 0;

(b) 2; 6; 18; 54; 162;

(c) 1; 1; 0; 1; 1; 0; 1; 1; 0;

4. Jon has a jar with 70 Tuna TreatsTM and 30 Me-WowsTM to give out to his cats, Fluy, Muy and Zazzles. How many ways can Jon give out the treats so that Fluy gets no Tuna TreatsTM, Muy gets 4 or more Tuna TreatsTM and 5 or more Me- WowsTM, and Zazzles get an odd number of Tuna TreatsTM?

5. Use generating functions to count the number of six-digit (positive) integers whose digits sum to 42. For example, 978468 is a six-digit integer whose digits sum to 9 + 7 + 8 + 4 + 6 + 8 = 42.

6. Evaluate the closed form generating function for the sequence a₀; a₁; a₂; : : : , where an is the number of partitions of the nonnegative integer n into

(a) even summands.

(b) distinct odd summands.

(c) summands that do not exceed 10 and occur at most 3 times.

(d) summands where summand 1 occurs at most once, summand 2 occurs at most twice, and in general, summand k occurs at most k times.