Reference no: EM13678526

Question 1: Graph, for -5 ≤ t ≤ 5, the following two continuous-time functions:

(a) g(t) = rect (t/3) + sin(4Πt + 2) and (b) g(t) = ramp(t)* sin(2Πt).

Question 2: Let a function be given by: g(t) = 4 t cos(10Πt), -2 ≤ t ≤ 2. Without analytically evaluating them, plot

(a) the even part of the function g(t)
(b) the odd part of the function g(t).

Question 3: Evaluate the average power for the signals:

(a) x(t) = 2 sin(200Πt)
(b) The periodic signal, with fundamental period T₀ = 6, described over the time period 0 < t < 6 by

x(t) = rect(t-2/3)-4rect(t-4/2)

Question 4: Graph the following discrete-time functions:

(a) g[n] = 10 ramp[n/2] , for -5 ≤ n ≤ 10

(b) g[n] = Σⁿ_m=0 cos(2Πm/12)u[rn], for 0 ≤ n ≤ 36.

Question 5: Graph the following discrete-time functions: n < 0

(a)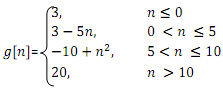   

 

(b) g[n/2]

Question 6: Graph the following functions:

(a) g [n] = u[n] - 0.5u[n - 7]

(b) h[n] = u[n] - u[n - 4]

(c) Y[n] = g[n] * h[n]

Question 7: Use MATLAB to find and to graph the unit-sequence response of the system given below

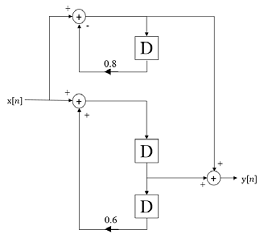
Question 8: A periodic signal x(t), with a fundamental period of 2 second, is described over one fundamental period by

 

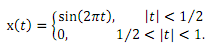
(a) Graph this signal over 2 fundamental periods.

(b) On the same plot, graph its Fourier series representation x_N(t) given by

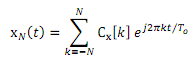
for N = 2, 4 and 10.

Question 9: A discrete-time signal is given by x[n] = sinc(n/8). Graph the magnitude and phase of the DTFT of x[n - 2] for the frequency range -0.5 to 0.5.

Note : In the sum, use n = -N:N, with N = 100,000.

Question 10: Graph the magnitude and phase of the DTFT of the signals x[n] and y[n]) (here y[n] is just a frequency shifted version of x[n]

(a) x[n] = cos(Πn/2), 0 ≤ n ≤ 100

(b) Y[n] = e^∫Πn/4x[n].

Note: For both graphs, plot over the frequency range -1 to 1.