Reference no: EM132429354

Assignment

Question 1. As shown in the figure below, a camera is mounted on a point 30 m from the base of a rocket launching pad. The rocket rises vertically when launched, and the camera's angle is continually adjusted to follow the base of the rocket.

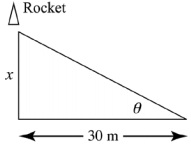
a. Express the height x as a function of the elevation angle θ.

b. give the domain of the function in part a.

c. give the height of the rocket when the elevation angle is Π/3.

Question 2. Consider the graphs of the functions f and g shown in the figure below.

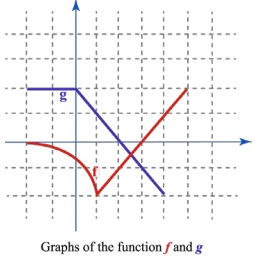
a. fill in the table below with the corresponding values of f and g.

x	-2	-1	0	1	2	3	4	5
f (x)
g(x)

b. Use the table in part a to evaluate each of the expressions listed below.
i. g o f (-2)
ii. g o f (1)
iii. g o f (4)
iv. f o g(0)
v. f o g(4)
vi. f o g(-1)

Question 3. Let f (x) = √(1 - 2x), g(x) = x/(x² - 1). find the formulas for the functions listed below and specify their respective domains.

a. f/g
b. g o f
c. gf²

Question 4. Consider the graph of the function f shown below.

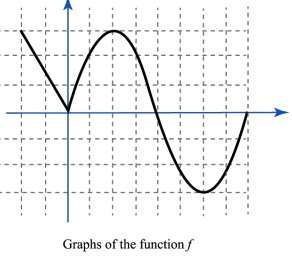
Apply the appropriate transformations and sketch the functions listed below. Aim for a neat, labeled graph.
a. f (x) = f (2x) - 1
b. g(x) = 1 - 2f (x)

Question 5. Indicate whether each of the limits listed below is well-defined. Explain your answer in each case.

a. lim_x→2 √(x² - 4)
b. lim_x→∞cot((x² + 1)/(x+3))

Question 6. Determine whether the evaluation of the limits given below are correct. If it is correct, explain why. If not, give the correct evaluation.

a. for x → -∞ we have √(x² - x³⁾/x = (√(-x³⁾√1-1/x)/x, hence

= lim_x→-∞√(x² - x³⁾/x = lim_{x →-∞} √-x³√1-1/x)/x = lim_{x →-∞} √(1 -1/x)√-x = ∞

b. lim_{x →0} x² sin(x - Π/2)/(1 - cos(3x)) = lim_{x →0} x² sin(x - Π/2) (1 + cos(3x))/((1 - cos(3x))(1 + cos(3x)))

= lim_{x →0} x² sin(x - Π/2) (1 + cos(3x))/(sin²(3x))

= lim_x→0 (x/sin(3x))²sin(x - Π / 2)(1 + cos(3x))

= lim_x→0 (x/sin(3x))² lim_x→0 sin(x - Π / 2)lim_x→0 1 + cos(3x)

= 1/9 (-1)(1)

= - 1/9

Question 7. Evaluate each of the limits listed below. Justify your answers by identifying the results of Units 2 and 3 you apply in each case. If a limit does not exist, explain why.

a. lim_{x →0} sin(Π - x)/√(x² - x + 1)

b. lim_x→3 (x3 - 3x² + 4x - 12)/(3x² - 7 x - 6)

c. lim_x→∞ cos((Πx+1)(3 -x²)/x³-Π)

d. lim_x→∞ xsin(3x)/(x² + 1)

e. lim_x+1+ sin(√x+1/(x² -1))

f. lim_{x →0+} √(x³+ x²)/(√(x+1) -1)

g. lim_{x →0} sin²(3x)/(1 - cos(2x)

Question 8. Let

          2/x                 if x < 0x

f (x)  = √x+ cos(Π x)   if 0 < x ≤ 5

            x/(x-5)          if x > 5

Evaluate the limits listed below. If a limit does not exist explain why.

a. lim f (x)
    x →0-

b. lim f (x)
   x →0+

c. lim f (x)
    x →5-

d. lim f (x)
   x →5+

e. lim f (x)
    x →5

f. lim f (x)
   x →∞

g. lim f (x)
   x →-∞
Where is the function not continuous? Explain.

Question 9. give the graph of one and only one function which satisfies all the following conditions.
a. Domain of the function [-5,0) ∪(0,∞)
b. The function is continuous on its domain
c. f (-5) = f (5)
d. lim f (x) = 6
x →5

e. lim f (x) = ∞
x →0-
f. lim f (x) = 0
x →0+
g. lim f (x) = -∞
x →∞
Explain why the graph of a function which satisfies all these conditions must intercept the x-axis, meaning that there is at least one number c so that f (c) = 0.

Question 10. Prove each of the statements below using the formal definition of limits.
a. If lim f (x) = -∞ and c > 0, then lim c f (x) = -∞.
       x →∞                                      x →∞
b. If lim g(x) = ∞ and g(x) ≤ f (x) for x → a, then lim f (x) = ∞.
       x →a                                                             x →a