Reference no: EM132267675
Problem 1 - The isomerization reaction A → B is carried out in a solvent with the help of a catalyst. The reaction scheme is thought to be:
1) A + S 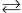 A·S
A·S
2) A·S 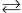 B·S
B·S
3) B·S 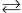 B + S
B + S
To investigate this reaction, you used a small, laboratory-scale reactor, dissolving various amounts of pure A in the solvent, and measured the initial net reaction rate rA0. At CA0 = 0.01 mol/kg-cat you observe a rate of rA0 = 10 mol/(s·kg-cat), and the rate varies linearly with CA0.
From the literature you collect the following kinetic parameters:
|
kads,A = 0.002 kg-cat/(s·mol)
|
kdes,A = 47.11 s
|
|
ks = 7.62 s-1
|
ks = 0.815 s-1
|
|
kads,B = 0.042 kg-cat/(s·mol)
|
kdes,B = 528.0 s-1
|
Questions -
a) Which step in the reaction scheme is rate-limiting, and why?
b) Estimate the total concentration of catalyst surface sites, CT.
c) Do you think that this estimate is a reasonable number? Why or why not?
Simplifying assumptions - Assume that the reaction is not limited by diffusion in any way.
Problem 2 - The exhaust gas of a combustor contains 1% of a toxic species A. You want to remove this contamination with the help of a porous catalyst in an isothermal packed bed reactor so that only 0.005 % of A are left. The net reaction is A → B + C, and the overall rate rA can be approximated as first-order.
Data
|
T0 = 900oC
|
P0 = 2 atm
|
|
|
k" = 2·10-10 m/s
|
Sa = 500 m2/g
|
|
|
De = 2·10-8 m2/s
|
cat = 3.2 g/cm3
|
cat. Pellet diameter = 1cm
|
Questions -
a) How much catalyst do you need to clean up 1 m3 gas per hour? (Assume no external mass transfer limitation).
b) If you (very crudely) approximate pressure drop in the reactor by taking the pressure in the reactor as constant P = 1.5 atm, how would your answer to (a) change?
c) Without calculating, how would your answer change if you had catalyst pellets of half the diameter? One tenth of the diameter?
Problem 3 - You carry out the enzyme reaction SEP with the following mechanism in a small laboratory-scale reactor.
1) S+E k_1Sk_1E#
2) SE# HO2 k_2P+E
You start with a 1M solution of the substrate, add 0.1 M of enzyme, and observe an initial rate -rS = 4.81·10-5 mol/(L·s). After an hour the substrate concentration has decreased to 0.83 mol/L, and you measure a rate of -rS = 4.68·10-5 mol/(L·s). Assuming that K1 = 10 L/mol, what are the forward rate constants, k1 and k2?
Additional data -
MH2O = 18 g/mol
H2O = 1 g/cm3