Reference no: EM131021347

Section 1.1

Using a calculator or computer, graph the functions.  Describe briefly in words the interesting features of the graph including the location of the critical points and where the function in increasing/decreasing.  Then use the derivative and algebra to explain the shape of the graph.

1.  f(x) = x³ - 6x + 1

Try graphing the x values from -5 to 5 with the major unit of 1, and the y values from -40 to 40 with the major unit of 10.

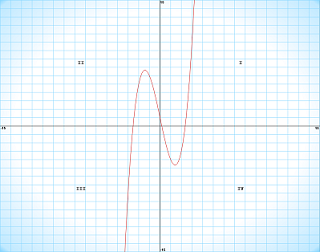
First Derivative: f'(x) = 3x² - 6 

Critical Points: f'(x) = 0

3x² - 6 = 0

3x²  = 6
x²  =2

x  = ±√2

x ≈ ±1.4142

The critical points divide our graph into how many regions? three 

X < -2.49                                 -1.41 < x < 1.41                                                          x > 2.4

You will now substitute a point from each of these regions into the derivative to determine whether the function is increasing or decreasing on that interval.

f'(x) = ??                                 f'(?) = ??                                             f'(?) = ??

f is ???                         f is ???                                                 f is ???

Second Derivative:     f''(x) = ???

You can now substitute your critical points into the derivative to determine if the graph is concave up or concave down at that point.

f''(?) = ???                                                                                          f''(?) = ???

Concave ???                                                                                        Concave ???

Local   Min/Max  Delete the incorrect one!                                        Local Min/Max 

Point:  (??, ?? )                                                                                    (??, ??)

2.  f(x) = x · In(x), x > 0

Try graphing the x values from 0.1, 1, 2, 3, 4, 5 with the major unit of 0.5, and the y values from -1 to 8 with the major unit of 1.

Please insert your graph here.

First Derivative: f'(x) = ???      

Critical Points: f'(x) = 0

?? = 0

x = ???

x ≈ ???

The critical point divides our graph into (how many?) regions:

X < ??                                                             x > ??

You will now substitute a point from each of these regions into the derivative to determine whether the function is increasing or decreasing on that interval.

f'(?) = ??                                                         f'(?) = ??

f is ???                                                 f is ???

You can now substitute your critical points into the derivative to determine if the graph is concave up or concave down at that point.

Second Derivative:     f''(x) = ???

f''(?) = ??                   

Concave ???               

Local Min/Max (delete the incorrect one!)

Point:  (??, ??)

Section 1.2

Use the first derivative to find all critical points and use the second derivative to find all inflection points.  Use a graph to identify each critical point as a local maximum, a local minimum, or neither.

1.  f(x) = x⁴ - 8x² + 5

First Derivative:          f'(x) = ???                   Critical Points:  f'(x) = 0

??????? = 0

4x(?????) = 0

??? = 0 ????? = 0

x = ??              x² = ???

x = ±?????

Second Derivative:     f''(x) = ???

You can now substitute your critical points into the derivative to determine if the graph is concave up or concave down at that point.

f''(x) = ???                              f''(?) = ???                                          f''(?) = ???

Concave ???                            Concave ???                            Concave ???

Local   Min/Max                     Local   Min/Max                     Local   Min/Max

To find inflection points, you must set the second derivative equal to zero and solve it!

Inflection Points:        f''(x) = 0         ??????? = 0

4(????) = 0

??? = ???

???? = ???

x = ±√? / ?

x = ≈±???

Try graphing the x values from -4 to 4 with the major unit of 1, and the y values from -20 to 60 with the major unit of 20.

Please insert your graph here.

2.  For f(x) = x³ - 18x² - 10x + 6, find the inflection point algebraically.  Graph the function with a calculator or computer and confirm your answer.

First Derivative:          f'(x) = ???

Second Derivative:     f''(x) = ???

Inflection Points:        f''(x) = 0

????= 0

???? = ???

x = ???

Try graphing the x values from -4 to 20 with the major unit of 2, and the y values from -1000 to 500 with the major unit of 500.

Please insert your graph here.

Section 1.3

1.  For f(x) = x - ln(x), and 0.1 ≤ x ≤ 2, find the value(s) of x for which:

(a)  f(x) has a local maximum or minimum.  Indicate which ones are maxima and which ones are minima.

First Derivative:          f'(x) = ?????   0.1 ≤ x ≤ 2                  

Critical Points:            f'(x) = 0

??? = 0

??? = ???

x = ???

Second Derivative:     f''(x) = ??????? = ??????, 0.1 ≤ x ≤ 2

f''(?) = ???                 

Concave ???

Local   Min/Max (delete the incorrect one!)

There is much debate over labeling an endpoint of an interval as a "local" minimum or maximum.  Therefore, we will not classify x = 0.1 or x = 2 as such.

(b)  f(x) has a global maximum or global minimum.

Critical Point and End Point Values:  f(?) = ??          f(?) = ??           f(?) = ???

???  is the global max

???  is global min

2.  The distance, s, traveled by a cyclist, who starts at 1 pm, is given in Figure 4.34.  Time, t, is in hours since noon.

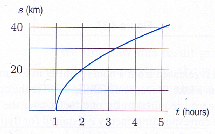
(a)  Explain why the quantity, s/t, is represented by the slope of a line from the origin to the point (t, s) on the graph.

(b)  Estimate the time at which the quantity s/t is a maximum.

At the point (?, ?), the value of s/t is ?? km/hr - ?:?? pm.

(c)  What is the relationship between the quantity s/t and the instantaneous speed of the cyclist at the time you found in part (b).

The quantity s/t is the ?????.