Reference no: EM132601419
MP4702 Advanced Materials and Materials Selection - University Of Central Lancashire
Obtain a material index for the elastic bending of a simply supported beam with uniform distributed load for the entire length of the beam for a circular cross section, d (where d - diameter of the beam). Both the length and stiffness of the beam are fixed by the design. The beam should not deflect more than δ under the bending load, F and the selected material should be as cheap as possible. The mid-point deflection, δ of an elastic beam of length, L loaded in three-point bending by a central load, F is given by:
δ = 5/384 FL3/EI
QUESTION A2
Boeing aerospace manufacture company is interested in analysing the failure of aircrafts due to fatigue. Boeing company has developed the in-house laboratory facility to test the aerospace materials for fatigue related failures. A group of designer engineer of the Boeing company planned to perform a series of fatigue test for a component made up of a steel. The fracture toughness of steel material under investigation was Kc = 90 MPa√m. In the process of fatigue testing, non-destructive testing technique by ultrasonic methods was followed. A crack of mm deep was observed by non-destructive testing. The crack growth rate under cyclic loading in the laboratory test condition was given by Paris relation
da = A (ΔK)m dN
The constants of the Paris equations were estimated to be A = 5 x 10-12 and m = 4, where σ is in MPa. Under the laboratory test condition, the steel component is subjected to an alternating
stress of range, Δσ = 220 MPa about a mean tensile stress of Δσ/2. Geometry factor in the fracture toughness expression, Y = 1.05 is assumed.
(i) At what critical length will fast fracture occur?
(ii) Estimate the number of cycles to failure.
(iii) Estimate the number of cycles to failure if the alternating stress range of the component is changed from Δσ = 220 MPa to ?σ = 250 MPa. All other parameters are kept constant.
QUESTION A3
(i) The British Plastics Federation (BPF) is the world's longest running plastics trade association, established in 1933 to represent the UK industry. BSF want to support the education institution along with the industrial partner to support the setting up the polymer laboratory in the universities. In the process of setting up the injection moulding machine in UCLAN a trial experiment was conducted on the thermosetting plastics. A force, F will inject a given weight of an epoxy thermosetting polymer into intricate mould of the injection moulding machine in two different time and temperature scale, i.e., 30 s at 180 degrees Celsius and in 85 s at 162 degrees Celsius. If the viscosity of the epoxy thermosetting polymer follows an Arrhenius law of diffusion, with a rate of process proportional to exp (- Q/RT ) m2 s-1, calculate how long the process will take at 237 degrees Celsius.
(ii) Discuss the possible behaviour of this material in relation to creep and compare it with the possible behaviour of a thermoplastic taking into consideration the main polymer structure characteristic of both. Compare the equation to model the injection with the equation to model creep.
[Hint] Give you answers with no more than 3 decimal places.
QUESTION A4
Phase diagram is a graphical representation of the physical states of a substance and it summarise the equilibrium constitution of an alloy system. A binary phase diagram of the copper-zinc system including brass is shown in the Figure Q - A4. Using the binary phase diagram of the Cu - Zn system list out the salient features by answering the following questions:
(i) List out the compositions and temperatures of the eutectoid point, and five peritectic points present in the binary Cu - Zn system.
(ii) What distinguishes the two alloys (70/30 brass and 60/40 brass) in the binary Cu - Zn system?
(iii) What roughly is the melting point of 70/30 brass in the binary Cu - Zn system?
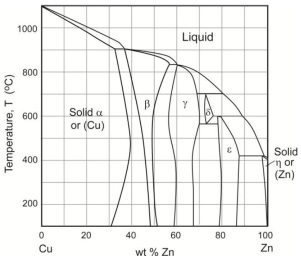
Figure Q - A4: Copper - Zinc phase diagram
QUESTION A5
(i) A corrosion cell should exist for corrosion to occur. Using simple sketches, briefly explain a corrosion cell.
(ii) Blackpool Tower has developed problems of corrosion as seen in the Error! Reference source not found. - A5. Suggest two strategies to prevent/reduce the corrosion in the Tower after replacement of the corroded components by replacements made of the same material as the original. Justify your choice with examples and discuss their advantages and disadvantages.

A5: Photographic view of the Blackpool tower
SECTION B
QUESTION B1
MATERIAL SELECTION FOR WASHINGTON MONUMENT
The Washington Monument is made up of marble, granite and bluestone gneiss which is an obelisk structure (Figure Q - B1). It was the World's tallest monumental column structure from 1884 to 1889 when it was overtaken by the Eiffel Tower, Paris. It remains the tallest stone structure. The current project in a famous architectural firm is to build a modern obelisk structure similar to Washington Monument and to be the tallest solid structure in the World.

Figure Q - B1: Washington Monument
In order to set up the construction work of the monument we need to find out the cost of the obelisk structure materials. The height of the obelisk structure is fixed as it has to be higher than any other similar solid structure in the world. The width and breadth of the obelisk structure is not defined. For the initial selection of the material, the main constraint is that the obelisk structure should not buckle by its own weight (self-buckling). The cross section of the structure is (a) rectangular and (b) square.
a) Rectangular cross section
(i) Translate the problem and derive the performance index for a rectangular cross section.
(ii) Use CES EDUPack (Rebranded as Ansys Granta) to calculate the slope of the selection line and select the materially graphically.
b) Square cross section
(i) Translate the problem and derive the performance index for a square cross section.
(ii) Use CES EDUPack (Rebranded as Ansys Granta) to calculate the slope of the selection line and select the materially graphically.
The equation that gives the length of self-buckling is:
L3 = 8 EI/ρgA
where, L is the length, E is the young modulus, I is the second moment of area, ρ is the density, g is the standard acceleration due to gravity, A is the cross-section area.
I = bw3/12
b is the breadth and w is the width of the rectangular cross section.
I = w4/12
w is the width of the square cross section.
QUESTION B2
MATERIAL SELECTION FOR A SPLINE SHAFT OF AN AUTOMOBILE CHASSIS
A spline shaft in an automobile chassis of a hollow circular cross section is subjected to an axial, bending and torsion loading during operation. As a design engineer of the Ford motors you have been assigned a task of selecting a new high strength alloy steel material which has a superior property of the current materials with minimum weight and as cheap as possible. The maximum load applied on the chassis under torsion is fixed by the designer. The external diameter, ???? and length, L of the shaft is fixed. The wall thickness, ?? of the shaft is not defined. The selected shaft material should not fail by yielding and fast fracture in torsion.
(i) Translate the problem indicating function, objective, constraints and free variables
(ii) Derive the performance index.
(iii) Discuss the implication of two performance index for the selection of one material. Find the coupling line by making equal the cost calculated with the two indexes.
T/J = τ/R = Gθ/L
T - Applied torque in Nm
J - Polar moment of inertia (m4) = ∫∫y2 dA
τ - Shear stress (Pa) R - Radius (m)
G - Shear modulus (Pa) θ - Twist angle (rad)
L - Length of the shaft (m)
Assume the thickness is much smaller than the diameter of the shaft. Therefore:
J ≈ (R)2 · 2ΠRt
Area of the shaft,
A ≈ 2ΠRt
Maximum shear stress theory,
τ = σ/2
Fast fracture condition,
Kc = τ (Πac)1/2

Figure Q - B2: Torsion of shaft