Reference no: EM132903480

ENGIN 5511 Mine Surveying - Federation University Australia

Question 1. A line AB between the stations A and B was measured as 347.28 using a 20 m tape, too short by 0.05 m. Determine the following:

a. The correct length of AB,
b. The reduced horizontal length of AB if AB lay on a slope of 1 in 25, and
c. The reading required to produce a horizontal distance of 22.85 m between two pegs, one being 0.56 m above the other.

Question 2. A base line was measured by a tape suspended in catenary under a pull of 145 N, the mean temperature being 15°C. The lengths of various segments of the tape and the difference in level of the two ends of a segment are given in the Table below.

Bay/Span	Length (m)	Difference in level (m)
1	29.989	+0.346
2	29.985	-0.211
3	29.840	+0.311
4	29.910	-0.106

If the tape was standardized on the flat under a pull of 95 N at, 18°C determine the correct length of the line. The following also apply:
• Cross-sectional area of the tape = 3.35 mm²
• Coefficient of linear expansion = 0.9 × 10-2 per °C
• Young's modulus = 14.6 × 104 MN/m²
• Mean height of the line above M.S.L. = 52.76 m
• Radius of earth = 6370 km

Question 3. It is proposed to widen a highway by increasing the gradient of the side slope to 1 in 1.5. The difference in level between the bottom and top of the embankment at a critical section was measured as 15.2 m. The length of the embankment along the side slope was measured as 29.869 m using a steel tape under a pull of 151 N at a temperature of 27°C. Determine the additional road width that will be available with the new slope. The tape was standardized on the flat at 18°C under a pull of 47 N. The cross-sectional area of the tape is 6.4 mm2, E = 20.9 × 10⁴ MN/m2 and α = 1.12 × 10^-5 per °C.

Question 4. The depth of a mineshaft was measured as 833.56 m using a 1000 m steel tape having a cross-section of 10 mm2 and a mass of 0.08 kg/m. Calculate the correct depth of the mine shaft if the tape was standardized at a tension of 182 N. The Young's modulus of elasticity of the tape material is 19 × 10⁴ N/mm2 and g = 9.806 m/s².

Question 5. The following observations were made to measure the length of a base line AB using an EDM instrument.

Measured distance = 1552.206 m Elevation of instrument at A = 187.31 m Elevation of reflector at B = 206.35 m
Temperature = 25°CPressure = 752 mm of mercury

Calculate the correct length of AB and its reduced length at mean sea level. Take ns = 1.0002851, n0 = 296 × 10^-6 and R = 6370 km.

Question 6. The slope distance between two stations A and B measured with EDM when corrected for meteorological conditions and instrument constants, is 113.893 m. The heights of the instrument and reflector are 1.739 m and 1.839 m, respectively, above the ground. To measure the vertical angle a theodolite was set up at A, 1.665 m above the ground and a target at B having height above the ground as 1.632 m. The measured angle above the horizontal was + 4°22′18″. Determine
a. The horizontal length of the line AB. b.
To what precision the slope angle be measured:
i. if the relative precision of the reduced horizontal distance is to be 1/100000.
ii. if the reduced horizontal distance is to have a standard error of ± 1.8 mm.

Question 7. What is a two-peg test, how is it conducted?

Question 8. The following readings were taken with a level and 4 m staff. Draw up a level book page and reduce the levels by the height of collimation method. 0.578 B.M.(= 58.250 m), 0.933, 1.768,2.450, (2.005 and 0.567) C.P., 1.888, 1.181, (3.679 and 0.612) C.P., 0.705, 1.810.

Question 9. Reduce the levels of the stations from the readings given in question 8 by the rise and fall method.

Question 10. The following consecutive readings were taken with a level on continuously sloping ground at a common interval of 20 m. The last station has an elevation of 155.272 m. Rule out a page of level book and enter the readings. Calculate the following:
a. the reduced levels of the points by rise and fall method, and
b. the gradient of the line joining the first and last points.
0.425, 1.115, 2.905, 3.615, 0.535, 1.470, 2.815, 3.505, 4.445, 0.605, 1.925, 2.885.

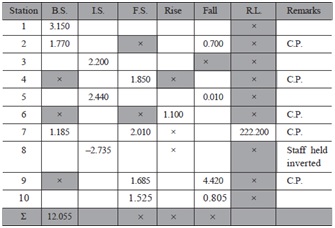
Question 11. A page of level book is reproduced on the following page in which some readings marked as (×), are missing. Complete the page with all arithmetic checks.

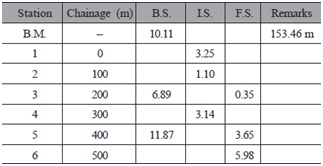
Question 12. Given the following data, determine the R.L.s of the points 1 to 6. If a uniform upward gradient of 1 in 20 starts at point 1, having elevation of 150 m, calculate the height of embankment and depth of cutting at all the points from 1 to 6.

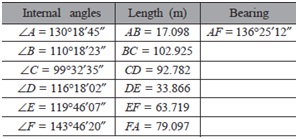
Question 13. The angles at the stations of a closed traverse ABCDEFA were observed as given below:

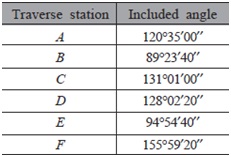
Adjust the angular error in the observations, if any, and calculate the bearings of the traverse lines in the following systems if whole circle bearing of the line AB is 42°:

Question 14. A closed-loop traverse ABCDA was run around an area and the following observations were made:

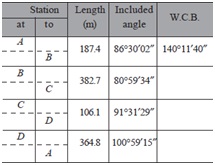
Adjust the angular error, if any, and calculate the coordinates of other stations if the coordinates of the station A are E1000 m and N1000 m.

Question 15. The data given below were obtained for an anti-clockwise closed-loop traverse. The coordinates of the station A are E1500 m and N1500 m. Determine the correct coordinates of all the traverse stations after adjusting the traverse by Bowditch's method.

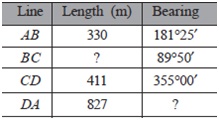
Question 16. The following data were collected while running a closed traverse ABCDA. Calculate the missing data.

Question 17. P, Q, R, and S are four stations whose coordinates are as below:

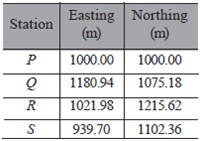
Another station X is to be fixed at the intersection of the lines PR and QS. What are the coordinates of X?

Question 18. The coordinates of two points are as follows:

Point	E (m)	N (m)
A	1577.58	7428.09
B	1235.71	7236.85

From A, a peg Z is placed in the ground such that AZ lies to the left of AB and makes an angle of 81°33'04" with it. The distance AZ is 127.83m. Compute the bearing and distance BZ.

Question 19. Horizontal angles were observed at a point P to three triangulation points A, B and C with the following results

Angle APB

80°09'17"

Angle BPC 54°46'56"

the angles being measured in a clockwise sense. The coordinates of the triangulation points are

Point	E (m)	N (m)
A	426047.73	564277.72
B	424461.40	563900.57
C	423227.92	564291.05

Calculate the coordinates of P.

Question 20. The following were the observed angles of a triangle ABC, the length of the side AB being 7619.82m.
A = 42°14'25"; B = 53°54'40"; C = 83°51'10"
Adjust the angles, and solve the triangle for the sides AC and BC

Question 21. It was required to lay out the line of a tunnel between two points A and D which were not intervisible; the points were joined by two triangles ABC and BCD of which the observed angles were:
Triangle ABC

A = 48° 15' 20"; B = 67°39'55"; C = 64°04'30"
Triangle BCD

B = 71°14'30"; C = 44°38'10"; D = 64°07'50"
The points A and D lie on opposite sides of BC, and the measured length of the side AB was 3246.33
m. Find the distance AD, and the angle BAD which must be set out on a theodolite in order to set the instrument on the correct alignment for setting out the line AD.

Question 22. Levelling carried out at an open cast coal site yielded the following results:

Grid Co-ordinates		Ground Level (m)
Easting	Northing
100	100	87.6
200	100	89.0
300	100	90.0
100	200	88.4
200	200	89.7
300	200	90.8
100	300	89.3
200	300	90.6
300	300	91.9

A borehole at coordinates (200,200) has revealed that the top of the coal seam 1.68 m thick is located 8.4 m below ground level. The seam is known to dip towards the north at a gradient of 1 in 50.
i. Calculate the volume of overburden contained in the gridded area
ii. If the ground level rises to the north at a mean gradient of 1 in 80 from 300 mN and the maximum ratio of overburden thickness for economic working is 15 to 1, estimate the grid Northing at Easting 200 m to which an east to west working face may be advanced before the site becomes uneconomic.

Question 23. It is proposed to sink a vertical shaft to connect X on a roadway CD in the upper horizon with a roadway GH in the lower horizon which passes under CD. From surveys in the two horizons the following data are compiled:

Upper horizon

Station	Horizontal Angle	Inclination	Inclined length (m)	Remarks
A				Coordinates of A 1996.166mE, 413.382mN   Bearing AB N 30°14'00"
		+ 1 in 200	260.412
B	276°15'45"
		+ 1 in 400	287.490
C	88°19'10"
		Level	224.397
D

Lower horizon

Station	Horizontal Angle	Inclination	Inclined length (m)	Remarks
E				Coordinates of E 2348.204mE, 369.076mN Bearing EF N 54°59'10"
		+ 1 in 50	99.417
F	193°46'45"
		+ 1 in 20	84.936
G	83°03'10"
		Level	190.835
H

Calculate the coordinates of X

Question 24. A shaft is sunk to a certain seam in which the workings have reached a level DE.
It is proposed to deepen the shaft and connect the point E in the dip workings to a point X by a cross measures drift, dipping at 1 in 200 towards X. The point X is to be 40.8 m from the centre of the shaft A and due East from it , AX being level. The following are the notes of a traverse made in the seam from the centre of the shaft A to the point E.

Line	Azimuth	Distance (m)	Vertical Angle
AB	270° 00'	38.7	Level
BC	184° 30'	167.7	Dipping 21°
CD	159° 15'	222.5	Dipping 18.5°
DE	90° 00'	25.3	Level

Calculate

i. The azimuth and horizontal length of the drift EX
ii. The amount by which it is necessary to deepen the shaft

Question 25. What types of traverse survey can be undertaken?

Attachment:- Mine Surveying.rar