Reference no: EM132392581

ELEE 5400 Computational Intelligence Techniques

ASSIGNMENT

Question_1:

Consider the following two membership functions A and B defined as follows:

A: Triangular membership function at 3, 6, 8 crisp values

B: Generalized Bell Shaped Membership Function at 1, 3, 7 crisp values,

Using Matlab (fuzarith) Toolbox in Matlab, create a script and plot the following fuzzy arithmetic operations:

1- Fuzzy addition A+B

2- Fuzzy addition A+B’

3- Fuzzy Product A.B, Note: experiment with more than algebraic product

4- Fuzzy division A\B

Question_2:

Assume X = N is a set of natural numbers, Given the following fuzzy set A ⊆ X

a) The set of real numbers “close to number 7” is defined by the following membership function:

μA(x) = 1/(1+(x-7)²

b) Another way of defining the above membership function could be defined as follows:

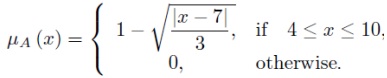
1- For parts a and b, Derive the fuzzy set A for the crisp values from 4 to 10

2- Plot the two methods of knowledge representation using the above mentioned fuzzy sets, i.e. the two membership functions:

Question_3:

Consider following three imprecise statements:

1) “low speed of the car”,

2) “medium speed of the car”,

3) “high speed of the car”.

Consider the universe of discourse X: [0, x_max] where x_max is the maximum speed

Create the membership functions graph illustrating fuzzy sets A, B, C corresponding to the above statements as follows:

• Set A is of the L type,

• Set B is of the T type,

• Set C is the class γ (Gamma).

• Consider 3 speeds: 30, 50 and 70 mph

Question_4:

Given the following fuzzy sets:

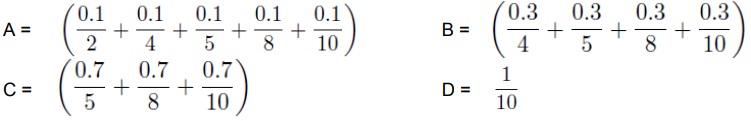
Find: the following fuzzy set decompositions:

1. A ∩ B ∩ C ∩ D,

2. A ∪ B ∪ C ∪ D,

3. A · B . C . D

Question_5:

Consider the following universe of discourse X = {1, 2, 3, 4, 5, 6, 7}

A = 0.9/3 + 1/4 + 0.6/6

B = 0.7/3 + 1/5 + 0.4/6

Find: A ∩ B, A ∪ B, and A · B (for Algebraic product, any other product would be acceptable)

Question_6:

The fuzzy relation R between the two sets X and Y is given by:

R = {((x, y) , μR (x, y))} , ∀ x∈X∀ y∈Y, μR : X × Y →[0, 1]

Given: X = {3, 4, 5} and Y = {4, 5, 6}

Using the following definition for R to formalize the following imprecise statement:

“y is more or less equal to x ”:

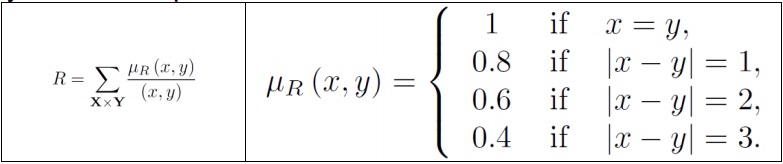
a) Create the fuzzy set R based on the mentioned membership format

R = Σ_x×y (μR (x,y) / (x,y))

b) Create the fuzzy set R in Matrix Format: (y1, y2, y3: RAWS, x1, x2, x3: Columns)

Question_7:

Given the following universe of discourse X = {1, 2, 3, 4, 5, 6}, and the fuzzy set A as follows:

A = 0.3/2 + 1/3 + 0.7/5 + 0.9/6

a) Find the complement of the set A:

b) Given the following new universe of discourse X = {1, 2, 3, 4}, and the fuzzy set A as follows:

A = 0.4/2 + 0.7/3 + 1/4

Find CONA(A) and DIL(A)

Question_8:

Assume that relations R and S are represented by matrices as follows:

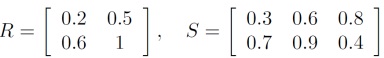
X = {x1, x2} Y = {y1, y2} Z = {z1, z2, z3}.

Determine the max-min type composition of the relations R and S: Q = R ? S

Question_9:

Arrange the following steps applied in fuzzy control in the right order, you can just re-write the step numbers in the right order:

1. Convert the output data to non-fuzzy values

2. Construct the rule base

3. Evaluate the rules in the rule base

4. Combine the results of each rule

5. Define the linguistic variables and terms

6. Convert crisp input data to fuzzy values using the membership functions

7. Construct the membership functions

Question_10:

Create a full FIS using Matlab FIS toolbox based on the following info:

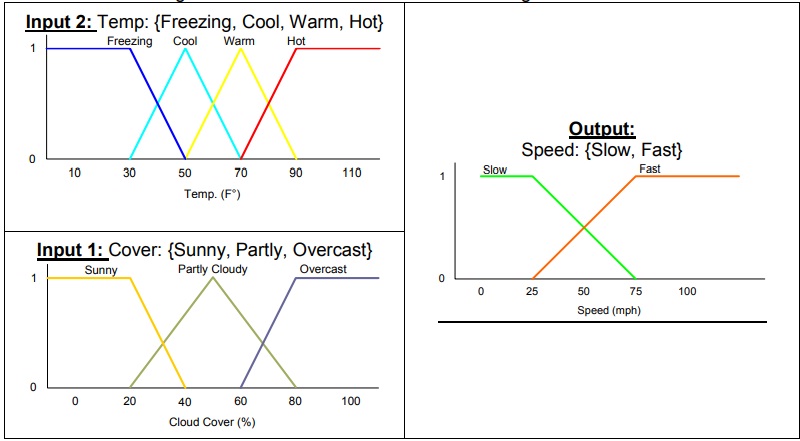
Rules:

R1: If it's Sunny and Warm, drive Fast

Meaning: Sunny(Cover) Λ Warm(Temp)Fast(Speed)

R2: If it's Cloudy and Cool, drive Slow

Meaning: Cloudy(Cover) Λ Cool(Temp)Slow(Speed)

a) How fast will will be the speed based on the following inputs:

• 65 F°
• 25 % Cloud Cover?