Reference no: EM132611989

Assignment  - Electromagnetic field and wave propagation

Q 1. Using Biot Savart law derive an expression for H due to an infinitely long straight filament carrying a current of I amperes.

Q2. A square filamentary loop of 2m side is placed in Z=0 plane with its centre at the origin. If current of 10A is passing through the loop, find H at origin.

Q3. An infinite long current filament is placed along z-axis. The magnetic field intensity at point P (3,4,0) is 10(-0.8ax + 0.6ay) A/m. Find the current through the filament.

Q4. Find magnetic field at the centre of the square loop of side 2L carrying current I. The current flows in an anticlockwise direction.

Q5. If vector magnetic potential is A = A x²yza_x + y²zxa_y + z²xya_z Find the magnetic flux density at (-1,2,5). Also find flux through z = 1,0 ≤ x ≤ 1,-1 ≤ y ≤ 4.

Q6. Given that current density J = -10(sin 2Φe^-2z aΦ + cos 2Φe^-2za_z)A/m², m find the total current crossing the plane Φ = 2Π,0 < ρ < 1,0 < Z < 1

Q7. An air coaxial transmission line has a solid inner conductor of radius 'a' and a very thin outer conductor of radius b. Determine magnetic field intensities in inner and outside the transmission line.

Q8. Given that the vector potential A= 10sinθa_r, find the magnetic field H for μ_r = 2.

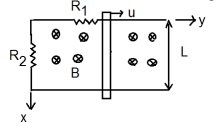
Q9. If B =0.1T, the position of the sliding bar as shown in Fig. in the y direction is given by y(t) = 0.1t, and L = 0.1m. Find the emf generated in the loop. If R₁=10ohm, R₂=20ohm, find the voltage drop across them and the current.

Q10. line X =0,y=0,0 ≤ z ≤ 10 carries current 2A along a_z^→ . Calculate H at (5,0,0) and (5,5,0).

Q11. Express A=10cos(10⁸t-10x+60° )a_z in phasor form.