Reference no: EM132711356

EG7033 Structural Dynamics and Stability - University of East London

The full-scale reinforced concrete (RC) frame shown in Figure 1 was subjected to the seismic excitation (dynamic type of loading) using a shake table. The experimental work was part of an EU funded research project that Dr Anca Ciupala participated in.

The dimensions of the frame, material properties and dimensions of the cross section of the structural elements (beams, columns, slab) are as follows:
• Span in each direction: 4.0 m
• Height of each floor: 3.3 m
• Beams: 260 x 400 mm
• Columns: 260 x 260 mm
• Slab: 120 mm thickness
• Concrete Young's modulus: 13500 MPa
• RC specific weight: 25 kN/m³
An additional mass of 4.5 tones is added at each floor of the frame.

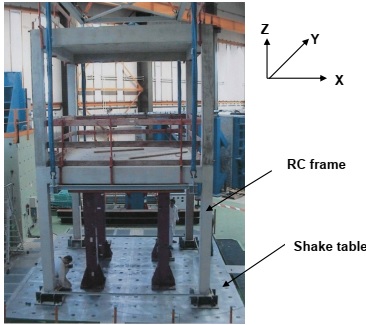
Figure 1. Reinforced concrete (RC) frame

The RC frame (named onwards as "bare frame") was subjected to a series of excitations as follows: white noise (to determine the natural frequencies of vibration of the newly cast concrete frame), followed by four uniaxial seismic excitations, applied in the X direction, of maximum accelerations 0.10 g, 0.20 g, 0.30 g and 0.40 g.

The natural frequencies of the bare frame obtained from the experimental testing, corresponding to the first two modes of vibration, are shown in Table 1.

Table 1. Experimental natural frequencies of vibration of the bare frame

Following the application of the four seismic excitations, the frame suffered an important level of damage which required strengthening. The selected strengthening technique was the confinement using Carbon Fibre Reinforced Polymers (CFRP), as shown in Figure 2.

Following strengthening with the CFRP material, the frame was again subjected to a series of excitations as follows: white noise (to determine the natural frequencies of vibration of the strengthened concrete frame), followed by three uniaxial seismic excitations, applied in the X direction, of maximum accelerations 0.20 g, 0.40 g and 0.50 g.

The natural frequencies of the strengthened frame obtained from the experimental testing, corresponding to the first two modes of vibration, are presented in Table 2.

Table 2. Experimental natural frequencies of vibration of the strengthened frame

Figure 2. RC concrete frame strengthened using CFRP material

Using the above information carry out the following:

1. Using the data provided in Tables 1 and 2, calculate the fundamental natural period of vibration determined experimentally for the bare and strengthened frame corresponding to each level of excitation applied (white noise and seismic excitations). Critically discuss the results obtained.

2. Assume that the bare frame shown in Figure 1 can be modelled using a simple dynamic model. Choose your own idealisation of a simple dynamic model and draw the corresponding mechanical model, clearly highlighting its main elements. Calculate by hand the natural periods of vibration of the simple model and clearly state all the assumptions made in your calculations.

3. Critically discuss the results obtained at point 2 above, particularly in relation to the results obtained experimentally (Table 1, White noise).