Reference no: EM1378322

We will be using a very robust, fast, and efficient automated inferencing system with support for disjuction and functions called DLV to practice with knowledge representation and reasoning. For many people, representing knowledge in a form that can be used by a computer for automated reasoning, although really just another form of computer programming, can seem rather difficult (much in the same way that some students happy to write 500 lines of C code fall apart when asked to write a 3-line Lisp/Scheme recursion :-)  In any case, there are other ways to conceptualize the act of programming besides "imperative" (C/Java/Pascal/Fortran-like) and "functional" (Lisp/Scheme/Racket/Scala/Haskell) programming. So-called "Logic Programming" or "Declarative Programming" is one of these other ways.

Example 1: Propositional Logic

Consider the following logic puzzle:

 Mr. Black, Mr. Red, and Mr. White were having a conversation.

"It's funny," said Mr. Black to the other two men, "that we are all wearing different colors, but none of us is wearing the color that is the same as his name."

"True," agreed another man, who was wearing white.

We can represent this in DLV with the following sentences:

% Proposition mrblack_wears_red means Mr. Black wears red.
% none wear color same as name disjunctive facts

mrblack_wears_red v mrblack_wears_white.
mrwhite_wears_red v mrwhite_wears_black.
mrred_wears_black v mrred_wears_white.
% alldiff constraints
:- mrblack_wears_red, mrwhite_wears_red.
:- mrblack_wears_white, mrred_wears_white.
:- mrwhite_wears_black, mrred_wears_black.
% the clue "...agreed another man, who was wearing white"
~mrblack_wears_white.

RareVosMBP:DLV decker$ ./dlv misterRBW.txt -nofacts
DLV [build BEN/Dec 17 2012 gcc 4.2.1 (Apple Inc. build 5666) (dot 3)]
{mrblack_wears_red, mrwhite_wears_black, mrred_wears_white}
{mrblack_wears_white, mrwhite_wears_red, mrred_wears_black}

But with the last sentence back in the KB, we get only a single model, the desired solution:

RareVosMBP:DLV decker$ ./dlv misterRBW.txt -nofacts
DLV [build BEN/Dec 17 2012 gcc 4.2.1 (Apple Inc. build 5666) (dot 3)]
{mrblack_wears_red, mrwhite_wears_black, mrred_wears_white}

First-Order Logic Example

Here is the Colonel West example from the book (Section 9.3.1) in dlv:

% "... it is a crime for an American to sell weapons to hostile nations"
criminal(X) :- american(X), weapon(Y), sells(X,Y,Z), hostile(Z).
% Nono has some missiles
missile(m1).
owns(nono,m1).
% All of its missiles were sold to it by Colonel West
sells(west,X,nono) :- missile(X), owns(nono,X).
% background: missiles are weapons.
weapon(X) :- missile(X).
% background: an enemy of America is "hostile" (to America)
hostile(X) :- enemy(X,america).
% "West, who is an American..."
american(west).

% "The country of Nono, an enemy of America..."
enemy(nono,america).
"
And the only model is the desired one, which includes the predicate criminal(west) as true:

RareVosMBP:DLV decker$ ./dlv west.txt -nofacts
DLV [build BEN/Dec 17 2012 gcc 4.2.1 (Apple Inc. build 5666) (dot 3)]
{criminal(west), weapon(m1), sells(west,m1,nono), hostile(nono)}

1. Getting Acquainted. Consider the following axioms:

• Horses are faster than dogs

• There is a greyhound that is faster than every rabbit

• Harry is a horse

• Ralph is a rabbit

We would like to prove Harry is faster than Ralph

1a. Write each sentence in FOL.

1b. Write any additional assumptions that you need (world knowledge) in FOL.

1c. Convert each sentence into CNF.

1d. Convert each sentence (or your CNF) into Datalog/DLV format.

1e. By hand, do a resolution proof with the CNF version that Harry is faster than Ralph. (show your work)

1d. Use DLV to prove the same thing (e.g. Harry is faster than Ralph in all models)

2. Three people, Amy, Bob, and Cal, are each either a liar or a truth-teller. Assume that liars always lie, and truth-tellers always tell the truth. 

• Amy says, "Cal and I are truthful."
• Bob says, "Cal is a liar."
• Cal says, "Bob speaks the truth or Amy lies."

What can you conclude about the truthfulness of each?

3. Use DLV to solve problem 5 on HW#2 (the "Sara had quadruplets" problem).

4. Use DLV to play the game Mastermind.

You should have a set of rules about the game in general (the intensional KB), and a set of speci?c facts about a speci?c game (the set of guesses and their responses). Probably the best way to think about this is that you are trying to compute all the models of the game rules and given facts. If there is only one model, then that is the solution.

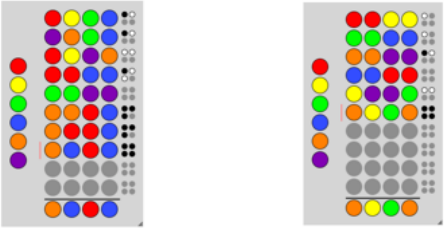
Develop a predicate BestGuess(color,color,color,color) that tells you what to guess next (even if there is no unique solution yet). At this point you have essentially written a full game player, although I am not asking you to hook the inputs and outputs together.