Reference no: EM133045587

ECE 8010 Analysis of Linear Systems - Clemson University

Question 1. Consider the following system

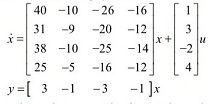
Note: choose integer entries for matrices whenever possible. If some matrices require non-integer entries, please write those entries as either (preferably) fractions or decimals to 4 significant digits.

a. Compute bases for the controllable and uncontrollable subspaces of the system.
Compute the bases "by hand". (You may use Matlab for basic computation and rref). Pick basis vectors with no fractions and as many zero entries as possible.

b. Does an input u(.) exist that can drive the state from x(0) = [0 0 0 0]^T to x(1) = [0 1 2 0]^T? Justify your answer.

c. Does an u(.) exist that can drive the state from x(0) = [0 0 0 0]^T to x(1) = [2 -3 5 -1]^T? Justify your answer.

d. Convert the system to an equivalent dynamical in Kalman Controllable Canonical

Form using a change of basis x = P_cx¯₁, based on your bases from part a. Label the blocks of the resulting matrices appropriately. Be sure to include the change of basis.

e. Extract the controllable subsystem from KCCF of part d. Use a change of basis ¯x_c= P_ox¯₂to convert the controllable subsystem to Kalman Observable Canonical Form.

Label the blocks of the resulting matrices appropriately. Be sure to include the change of basis.

f. Based on parts b,c, use a change of basis to convert the system to Kalman Canonical Form. Label the blocks of the resulting matrices appropriately. Be sure to include the change of basis.

g. List the eigenvalues of the system. For each eigenvalue, indicate whether it is associated associated with the controllable and obervable subspace, the controllable and unobservable subspace, or the uncontrollable subspace.

h. Calculate and simplify by hand the matrix transfer function for the system in Kalman Canonical Form. (Use appropriate shortcuts to make the calculation easier. You may use Matlab to check your answer, but ) Calculate the matrix transfer function for the original system using symbolic computation. Compare the matrix transfer functions for the original system and KCF system.

i. Is the original system BIBS stable? Justify your answer.

j. is the original system stabilizable? Justify your answer.

Question 2. Consider the system

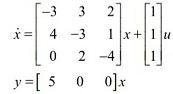
a. Design a full state feedback law u = -Kx + v so that the closed loop system has eigenvalues at -8,-8,-8. (You may use Matlab to assist with calculations, but do not use Ackermann's formula or the Matlab place command.)

b. Design an observer with gain L such that the error dynamics has eigenvalues at -3, -5, -7. (You may use any method to design the observer.)

c Write down the combined system with observer feedback, i.e., u = -Kx + v, using state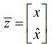. The output for the combined system is the output y of the x original system. (That is, do not include output of the observer P.)

d. Consider the following initial conditions of the combined system, z₀₁ = [1 1 2 0 0 0]^T Or and z₀₂ = [1 1 2 1 1 2]^T. Simulate the combined system from part c with zero input for each of the two different initial conditions z01 z02 Submit a clearly labeled plot showing the output y over time for the two different initial conditions (include both ouputs on the same plot for easier comparison) (See matlab commands ss and initial.)

e. Simulate the combined system from part c for each of the initial conditions z₀₁, z₀₂, from part d but with periodic square wave input (see below for Matlab commands to implement a periodic square wave with period 2). Submit a clearly labeled plot showing the output plot y over time for the two different initial conditions (include both ouputs on the same plot for easier comparison). (See matlab command lsim)

f. Discuss the similarities and differences for the plots from parts d and e. Discuss how the plots match (or don't ) the theoretical expectations for how a system with observer feedback should behave.

The following code can be used to implement a periodic square wave with period 2 in matlab.

tt = linspace(0,6,1000); % vector of time values
u = (mod(tt,2)<1); % periodic square wave, period 2

Question 3. The dynamics of the double pendulum on cart are given by

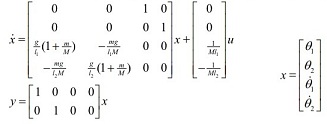
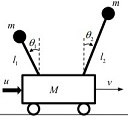
The system parameters are M =10, m =1, l₁=1, g =9.8.

a. For l₂ = 5, design a feedback controller u = -K₁x to place the closed loop eigenvalues at -1± j, -2, -3. (You may use Matlab)

b. For l₂ = 1.01, design a feedback controller u = -K₂x to place the closed loop eigenvalues at -1± j, -2, -3. (You may use Matlab)

c. Discuss why the gain vectors are so different in (a) and (b), taking into system properties such as stability, controllability, observability as appropriate. What does this mean for practical implementation of these controllers?