Reference no: EM132904095

DSC-510 Advanced Probability and Statistics - Grand Canyon University

Discussion Questions

1. Use the R command X <- iris to assign Fishers' iris dataset to the data matrix X. Using the head(X) command summarize what each column of the dataset is measuring and represents. Assign Y as a new matrix of dimension 150 by 4 which has the values of X without the species label.

2. Compute and interpret (in summary English) each of the summary statistics X ¯,S,Rusing R.

3. Visualize the dataset by making a scatterplot of Sepal Length vs. Sepal Width, a scatterplot of Petal Length vs. Petal Width. The pairs function and page 422 is useful here. Use your plots and stats from #2 to comment on any evident correlations.

Numerical Questions

Instructions: Answer the following using the R statistical computing platform. Your answer should include the code you wrote plus the output of such code and English rhetoric / coding comments where necessary.

N1. The iris dataset is a native dataset to R. Obtain a matrix of scatter plots for the overall dataset (without species), and the three subsets according to species. Obtain an average of the four characteristics by species and, using the faces function from the aplpack package, plot the Chernoff faces. Do the Chernoff faces offer enough insight to identify the group?

N2. Equation 14.7 gives the Mahalanbonisdistance. Use this to obtain the "distance" of the observations from the entire dataset for the board stiffness dataset and investigate for outliers. Repeat this for the iris dataset as well.

Iris Dataset

Theoretical Questions

Instructions: Answer the following in a mathematically sound argument (proof) using combinations of English / symbols as needed.

T1. Let Y be a random vector with the following mean vector and variance/covariance matrix:

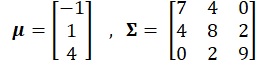
Define the univariate transformations x=y₁-3y₂+y₃, z₁=y₁+y₂+y₃ ,z₂=4y₁+y₂-y₃ . Form the random vector z=(z₁,z₂)'. Compute each of E(x),var(x),E(z),cov(z).

T2. Let X be drawn from a 3-dimensional normal distribution with mean vector μ'=[-1,0,4]and variance/covariance matrix:

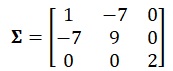
We want to determine what combinations or pairs of the random variables are independent. Determine if each pair of random vectors are independent:

X₁ and X₂
X₂ and X₃
(X₁,X₃ ) and X₂

Is it true that each of X₁,X₂,X₃ are individually univariate normal given that Xis multivariate normal? Give reasoning on why or why not.